Når du studerer fysikk i 10. klasse, vurderes temaet dipoler. Hva betyr dette konseptet og hvilke formler brukes til å beregne det?
Introduksjon
Hvis du plasserer en dipol i rommet til et jevnt elektrisk felt, kan du representere den som kraftlinjer. En dipol er et system der det er to ladninger som er identiske i parametere, men de er motsatte punktladninger. Dessuten vil avstanden mellom dem være mye mindre enn avstanden til et hvilket som helst punkt i dipolfeltet. Konseptet med dipolmomentet studeres i skolekurset i elektrodynamikk (10. klasse).
Aksen til dipolen er en rett linje som går gjennom punktene til begge ladningene. En dipolarm er en vektor som forbinder en ladning og samtidig går fra negativt ladede partikler til positivt ladede partikler. En elektrisk dipol er karakterisert ved tilstedeværelsen av en tilstand som en dipol eller elektrisk moment.
Per definisjon er et dipolmoment en vektor som er numerisk lik produktet av dipolladningen og dens arm. Dessuten er den samrettet med skulderen til dipolen. Ved null likhet av summen av krefter, beregner vi verdien av momentet. For vinkelen som eksisterer mellom dipolmomentet ogretning av det elektriske feltet, tilstedeværelsen av et mekanisk moment er karakteristisk.
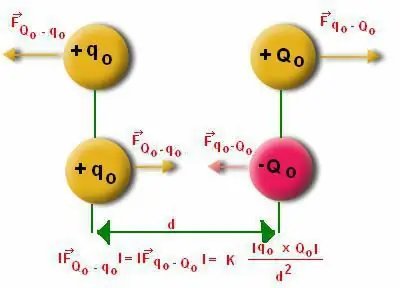
Ofte synes folk det er vanskelig å beregne modulen som virker på dipolstrukturen. Her er det nødvendig å ta hensyn til særegenhetene ved å beregne vinkelen "Alpha". Det er kjent at dipolen avviker fra den balanserte posisjonen. Men selve dipolmomentet har en gjenopprettende karakter, da det har en tendens til å være i bevegelse.
Beregninger
Når dette dipolmomentet plasseres i mediet til et inhomogent elektrisk felt, oppstår det uunngåelig en kraft. I et slikt miljø vil ikke indikatorene for summen av krefter være null. Følgelig er det krefter som virker på dipolmomentet med en punktkarakter. Størrelsen på dipolarmen er mye mindre.
Formelen kan skrives slik: F=q (E2 - E1)=qdE, der d er differensialen for det elektriske felt.
Søk etter egenskapene til det fysiske konseptet som studeres
La oss se nærmere på emnet. For å bestemme hva som er karakteristisk for det elektriske feltet, hvis det er opprettet ved hjelp av et ladningssystem og lokalisert i et lite rom, er det nødvendig å gjøre en rekke beregninger. Et eksempel er presentert av atomer og molekyler, som i sin sammensetning har elektrisk ladede kjerner og elektroner.
Hvis det er nødvendig å søke etter et felt i en avstand større enn dimensjonene som utgjør området der partiklene befinner seg, vil vi bruke en rekke eksakte formler som er svært komplekse. Det er mulig å bruke enklereomtrentlige uttrykk. La oss anta at punktsett med ladninger qk deltar i dannelsen av det elektriske feltet. De er plassert på en liten plass.
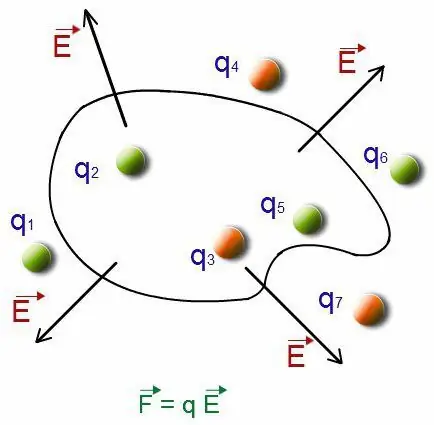
For å utføre beregningen av karakteristikken som feltet har, er det tillatt å kombinere alle ladningene til systemet. Et slikt system betraktes som en punktladning Q. Størrelsesindikatorene vil være summen av ladningene som var i det opprinnelige systemet.
Plassering av belastninger
La oss forestille oss at plasseringen av belastningen er angitt hvor som helst hvor belastningssystemet qk er plassert. Når du gjør endringer i plasseringen, hvis den har begrensninger uttrykt i et lite område, vil en slik påvirkning være ubetydelig, nesten umerkelig for feltet ved synspunktet. Innenfor slike grenser for tilnærming av styrke og potensial som det elektriske feltet har, gjøres det ved bruk av tradisjonelle formler.
Når summen av den totale ladningen til systemet er null, vil parametrene for den angitte tilnærmingen se grove ut. Dette gir grunn til å konkludere med at det elektriske feltet rett og slett er fraværende. Hvis det er nødvendig å oppnå en mer nøyaktig tilnærming, samle ment alt separate grupper av positive og negative ladninger av systemet som vurderes.
Ved forskyvning av deres "sentre" i forhold til andre, kan feltparametrene i et slikt system beskrives som et felt som har to punktladninger, like store og motsatte i fortegn. Det bemerkes at de er fortrengt i forhold til andre. Å skaffeFor en mer nøyaktig karakterisering av ladningssystemet når det gjelder parametrene for denne tilnærmingen, vil det være nødvendig å studere egenskapene til en dipol i et elektrisk felt.
Introduksjon av begrepet
La oss gå tilbake til definisjonen. En elektrisk dipol er definisjonen på et system som har to punktladninger. De har samme størrelse og motsatte tegn. Dessuten er slike skilt plassert i liten avstand i forhold til andre skilt.
Du kan beregne karakteristikken til prosessen som skapes ved hjelp av en dipol, og den er representert ved to punktladninger: +q og −q, og de er plassert i en avstand a i forhold til de andre.

Rekkefølge av beregninger
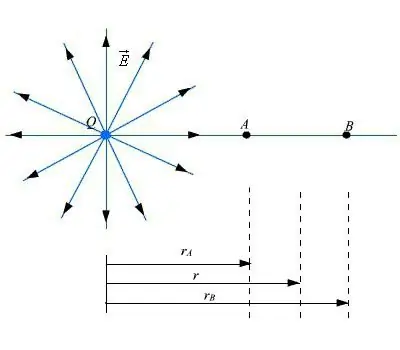
La oss starte med å beregne potensialet og intensiteten som dipolen har på sin aksiale overflate. Dette er en rett linje som går mellom to ladninger. Forutsatt at punktet A ligger i en avstand som er lik r i forhold til den sentrale delen av dipolen, og hvis det er r >> a, vil det i henhold til prinsippet om superposisjon for feltpotensialet på dette punktet være rasjonelt å bruk uttrykket for å beregne parameterne til den elektriske dipolen.
Størrelsen på styrkevektoren beregnes etter superposisjonsprinsippet. For å beregne feltstyrken brukes konseptet med forholdet mellom potensial og feltstyrke:
Ex=−Δφ /Δx.
Under slike forhold indikeres retningen til intensitetsvektoren på langs i forhold til dipolaksen. For å beregne modulen er standardformelen gjeldende.
Viktigavklaringer
Det bør tas i betraktning at svekkelsen av det elektriske dipolfeltet skjer raskere enn det opplever en punktladning. Nedfallet av dipolfeltpotensialet er omvendt proporsjonal med kvadratet av avstanden, og feltstyrken er omvendt proporsjonal med kuben av avstanden.
Ved bruk av lignende, men mer tungvinte metoder, blir parametrene for potensialet og feltstyrken til dipolen funnet på vilkårlige punkter, hvis posisjonsparametre bestemmes ved hjelp av en slik beregningsmetode som polare koordinater: avstanden til sentrum av den elektriske dipolen (r) og vinkelen (θ).
Beregning med spenningsvektor
Konseptet med intensitetsvektoren E er delt inn i to punkter:
- Radial (Er), som er rettet i lengderetningen i forhold til den rette linjen.
- En slik rett linje forbinder det spesifiserte punktet og sentrum av dipolen med perpendikulæren til den Eθ.
Denne dekomponeringen av hver komponent er rettet langs endringsforløpet som skjer med alle koordinatene til punktet som skal observeres. Du kan finne det ved forholdet som relaterer feltstyrkeindikatorer til potensielle modifikasjoner.
For å finne vektorkomponenten ved feltstyrken er det viktig å etablere sammenhengens natur i de potensielle endringene som oppstår på grunn av forskyvningen av observasjonspunktet i retning av vektorene.
Beregn den perpendikulære komponenten
Når ferdigFor denne prosedyren er det viktig å ta hensyn til at uttrykket for størrelsen ved en liten vinkelrett forskyvning vil bli bestemt ved å endre vinkelen: Δl=rΔθ. Størrelsesparameterne for denne feltkomponenten vil være like.
Etter å ha oppnådd forholdet, er det mulig å bestemme feltet til den elektriske dipolen på et vilkårlig punkt for å bygge et bilde med kraftlinjene til dette feltet.
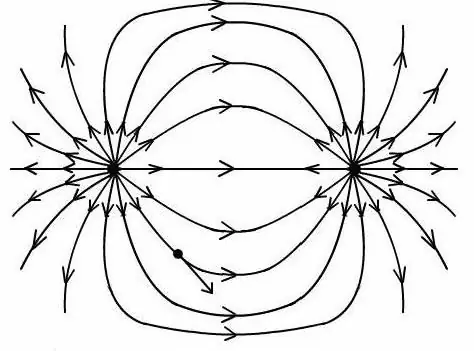
Det er viktig å tenke på at alle formler for å bestemme potensialet og feltstyrken til en dipol kun fungerer på produktet av verdiene som én dipolladning har og avstanden mellom dem.
Dipolmoment
Tittelen på det beskrevne arbeidet er en fullstendig beskrivelse av den elektriske typen egenskaper. Den har navnet "systemets dipolmoment".
Ved definisjon av en dipol, som er et system av punktladninger, kan man finne ut at den er preget av tilstedeværelsen av aksial symmetri, når aksen er en rett linje som går gjennom flere ladninger.
For å stille inn hele karakteristikken til dipolen, angi orienteringsretningen som aksen har. For enkelhets skyld kan dipolmomentvektoren spesifiseres. Verdien av dens størrelse er lik størrelsen på dipolmomentet, og retningsvektoren er forskjellig ved sammentreffet av den og dipolens akse. Så, p=qa hvis a er retningen til vektoren som forbinder de negative og positive ladningene til dipolen.
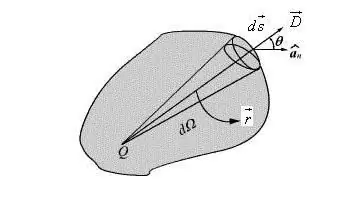
Bruk av en slik karakteristikk av dipolen er praktisk og gjør det i de fleste tilfeller mulig å forenkle formelen og gi den formenvektor. Beskrivelsen av potensialet til dipolfeltet i et punkt i en vilkårlig retning er skrevet i form av en vektor.
Introduksjonen av slike begreper som vektorkarakteristikken til en dipol og dens dipolmoment kan utføres ved å bruke en forenklet modell − en punktladning i et enhetlig felt, som inkluderer et system av ladninger, hvis geometriske dimensjoner gjør trenger ikke tas i betraktning, men det er viktig å kjenne dipolmomentet. Dette er en forutsetning for å utføre beregninger.
Hvordan en dipol oppfører seg
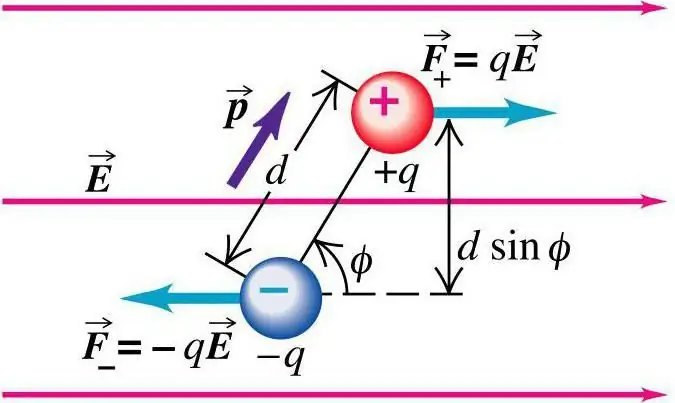
Atferden til en dipol kan sees på eksemplet med en slik situasjon. Plasseringen av to punktladninger har en fast karakter av avstand i forhold til hverandre. De ble plassert under forholdene til en dipol med et jevnt elektrisk felt. Gjorde observasjoner på prosessen. I leksjonene i fysikk (elektrodynamikk) blir dette konseptet vurdert i detalj. Fra feltet til ladningen utføres krafthandlingen:
F=±qE
De er like store og motsatte i retning. Indikatoren for den totale kraften som virker på dipolen er null. Siden en slik kraft har en effekt på forskjellige punkter, vil det totale momentet være:
M=Fa sin a=qEa sin a=pE sin a
med α er vinkelen som forbinder feltstyrkevektorene og dipolmomentvektorene. På grunn av tilstedeværelsen av et kraftmoment, har dipolmomentet til systemet en tendens til å gå tilbake til retningene til den elektriske feltstyrkevektoren.
Elektrisk dipol er et konsept som er viktig å forstå tydelig. Du kan lese mer om det på Internett. Det kan ogsåå studere i fysikktimene på skolen i 10. klasse, som vi snakket om ovenfor.






