I fysikk studeres temaet parallell- og seriekobling, og det kan ikke bare være ledere, men også kondensatorer. Det er viktig her å ikke bli forvirret over hvordan hver av dem ser ut på diagrammet. Og først da bruk spesifikke formler. Du må forresten huske dem utenat.
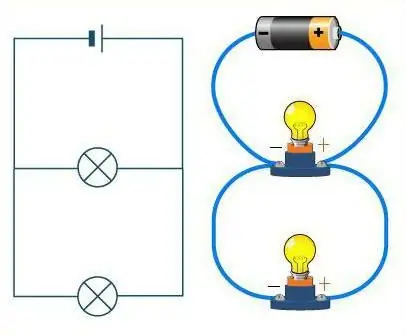
Hvordan skille mellom disse to forbindelsene?
Ta en nærmere titt på diagrammet. Hvis ledningene er representert som en vei, vil bilene på den spille rollen som motstander. På en rett vei uten gafler kjører biler etter hverandre, i kjetting. Seriekoblingen av ledere ser også lik ut. Veien kan i dette tilfellet ha et ubegrenset antall svinger, men ikke et enkelt kryss. Uansett hvordan veien (trådene) logret, vil maskinene (motstandene) alltid være plassert etter hverandre, i én kjede.
Det er en ganske annen sak om en parallellforbindelse vurderes. Da kan motstandene sammenlignes med idrettsutøvere i starten. De erhver står på sitt eget spor, men de har samme bevegelsesretning, og målstreken er på samme sted. På samme måte, motstander - hver av dem har sin egen ledning, men de er alle koblet sammen på et tidspunkt.
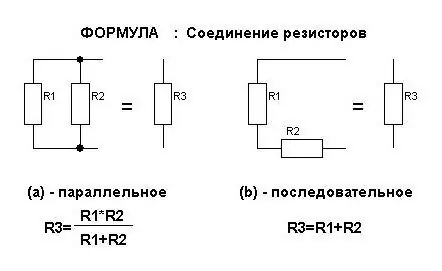
Formler for gjeldende styrke
Det diskuteres alltid i temaet "Elektrisitet". Parallell- og seriekoblinger påvirker strømmengden i motstander på forskjellige måter. For dem utledes formler som kan huskes. Men det er nok bare å huske betydningen som er investert i dem.
Så, strømmen i seriekobling av ledere er alltid den samme. Det vil si at i hver av dem er verdien av den nåværende styrken ikke forskjellig. Du kan tegne en analogi hvis du sammenligner en ledning med et rør. I den renner alltid vann på samme måte. Og alle hindringer i veien vil bli feid bort med samme kraft. Samme med gjeldende. Derfor ser formelen for totalstrømmen i en krets med seriekobling av motstander slik ut:
I gen=I 1=I 2
Her angir bokstaven I styrken til strømmen. Dette er en vanlig notasjon, så du må huske den.
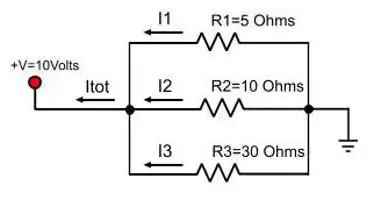
Strøm i parallellforbindelse vil ikke lenger være en konstant verdi. Med samme analogi med et rør, viser det seg at vannet vil deles i to bekker dersom hovedrøret har en forgrening. Det samme fenomenet observeres med strøm når en forgrening av ledninger dukker opp i veien. Formelen for total strømstyrke når lederne er parallellkoblet:
I gen=I 1 + I 2
Hvis forgreningen består av ledninger sommer enn to, så vil det i formelen ovenfor være flere termer med samme tall.
Formler for stress
Når det vurderes en krets der lederne er koblet i serie, bestemmes spenningen i hele seksjonen av summen av disse verdiene på hver spesifikk motstand. Du kan sammenligne denne situasjonen med plater. Det vil være lett for en person å holde en av dem, han vil også kunne ta den andre i nærheten, men med vanskeligheter. En person vil ikke lenger kunne holde tre tallerkener ved siden av hverandre, hjelp av en andre vil være nødvendig. Etc. Folks innsats går opp.
Formelen for den totale spenningen til en seksjon av en krets med seriekopling av ledere ser slik ut:
U gen=U 1 + U 2, hvor U er den vedtatte betegnelsen for elektrisk spenning.
En annen situasjon oppstår hvis en parallellkobling av motstander vurderes. Når tallerkener er stablet oppå hverandre, kan de fortsatt holdes av én person. Så du trenger ikke å legge til noe. Den samme analogien observeres når lederne er koblet parallelt. Spenningen på hver av dem er den samme og lik den som er på dem alle samtidig. Formelen for total spenning er:
U gen=U 1=U 2
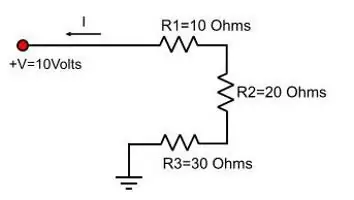
Formler for elektrisk motstand
Du kan ikke lenger huske dem, men kjenne formelen til Ohms lov og utlede den ønskede fra den. Det følger av denne loven atspenning er lik produktet av strøm og motstand. Det vil si U=IR, der R er motstanden.
Så formelen du må jobbe med avhenger av hvordan lederne er koblet sammen:
- i serie, så du trenger likestilling for spenning - IgenRtotal=I1R1 + I2R2;
- parallelt er det nødvendig å bruke formelen for strømstyrken - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Følgt av enkle transformasjoner, som er basert på at i den første likheten har alle strømmene samme verdi, og i den andre - er spenningene like. Så de kan forkortes. Det vil si at følgende uttrykk oppnås:
- R gen=R 1 + R 2 (for seriekobling av ledere).
- 1 / R gen=1 / R 1 + 1 / R 2(når parallellkoblet).
Når antall motstander koblet til nettverket øker, endres antallet termer i disse uttrykkene.
Det er verdt å merke seg at parallell- og seriekobling av ledere har en annen effekt på den totale motstanden. Den første av dem reduserer motstanden til kretsseksjonen. Dessuten viser det seg å være mindre enn den minste av motstandene som brukes. Når det er seriekoblet, er alt logisk: verdiene legger seg sammen, så det totale antallet vil alltid være størst.
Jobb nå
De tre foregående størrelsene utgjør lovene for parallellkobling og seriearrangement av ledere i en krets. Derfor er det viktig å kjenne dem. Om arbeid og kraft, du trenger bare å huske den grunnleggende formelen. Det er skrevet som følger: A \u003d IUt, der A er strømmens verk, t er tidspunktet for dens passasje gjennom lederen
For å bestemme det totale arbeidet med en seriekobling, må du bytte ut spenningen i det opprinnelige uttrykket. Du får likheten: A \u003d I(U 1 + U 2)t, åpne parentesene der det viser seg at arbeid på hele delen er lik beløpet for hver spesifikke nåværende forbruker.
Begrunnelsen fortsetter på samme måte hvis en parallellkoblingsordning vurderes. Kun strømstyrken skal erstattes. Men resultatet blir det samme: A=A 1 + A 2.
Gjeldende strøm
Når du utleder en formel for effekt (notasjon "P") for en kretsseksjon, må du igjen bruke én formel: P \u003d UI. Etter slike resonnementer viser det seg at parallell- og serieforbindelser er beskrevet av en slik formel for potens: P \u003d P1 + P 2.
Det vil si at uansett hvordan ordningene er lagt opp, vil den totale kraften være summen av de som er involvert i arbeidet. Dette forklarer det faktum at det er umulig å inkludere mange kraftige enheter i leilighetsnettverket samtidig. Hun tåler bare ikke belastningen.
Hvordan påvirker koblingen av ledere reparasjonen av nyttårskransen?
Umiddelbart etter at en av pærene er utbrent, blir det klart hvordan de ble koblet sammen. Påseriell tilkobling, vil ingen av dem lyse opp. Dette skyldes at en lampe som har blitt ubrukelig skaper et brudd i kretsen. Derfor må du sjekke alt for å finne ut hvilken som er utbrent, erstatte den - og kransen vil begynne å fungere.
Hvis den bruker en parallellkobling, slutter den ikke å fungere hvis en av pærene svikter. Tross alt vil kjeden ikke være helt ødelagt, men bare en parallell del. For å reparere en slik krans trenger du ikke sjekke alle elementene i kretsen, men bare de som ikke lyser.
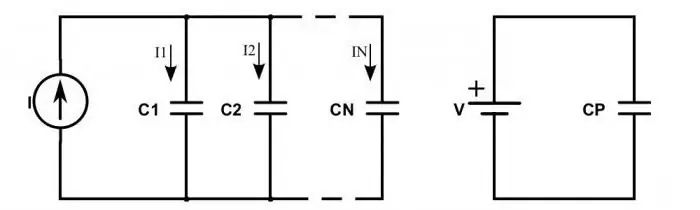
Hva skjer med en krets hvis kondensatorer er inkludert i stedet for motstander?
Når de er koblet i serie, observeres følgende situasjon: ladninger fra plussene til strømkilden kommer bare til de ytre platene til de ekstreme kondensatorene. De i mellom sender ganske enkelt den ladningen langs kjeden. Dette forklarer det faktum at de samme ladningene vises på alle platene, men med forskjellige fortegn. Derfor kan den elektriske ladningen til hver kondensator koblet i serie skrives som følger:
q gen =q 1=q 2.
For å bestemme spenningen på hver kondensator, må du kjenne formelen: U=q / C. I den er C kapasitansen til kondensatoren.
Total spenning følger samme lov som motstander. Derfor, ved å erstatte spenningen i kapasitansformelen med summen, får vi at den totale kapasitansen til enhetene må beregnes ved å bruke formelen:
C=q / (U 1 + U2).
Du kan forenkle denne formelen ved å snu brøkene og erstatte forholdet mellom spenning og ladning med kapasitans. Det viser seg følgende likhet: 1 / С=1 / С 1 + 1 / С 2.
Situasjonen ser noe annerledes ut når kondensatorene er koblet parallelt. Deretter bestemmes den totale ladningen av summen av alle ladninger som samler seg på platene til alle enheter. Og spenningsverdien bestemmes fortsatt i henhold til generelle lover. Derfor er formelen for den totale kapasitansen til kondensatorer koblet parallelt:
С=(q 1 + q 2) / U.
Det vil si at denne verdien anses som summen av hver av enhetene som brukes i forbindelsen:
S=S 1 + S 2.
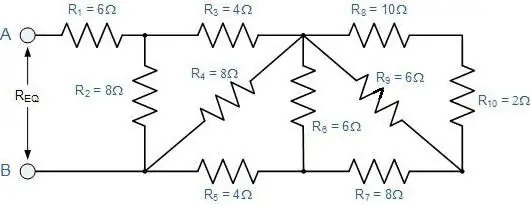
Hvordan bestemmer jeg den totale motstanden til en vilkårlig tilkobling av ledere?
Det vil si en der påfølgende seksjoner erstatter parallelle, og omvendt. For dem er alle de beskrevne lovene fortsatt gyldige. Bare du trenger å bruke dem i etapper.
Først er det ment å ment alt utvide ordningen. Hvis det er vanskelig å forestille seg det, må du tegne hva som skjer. Forklaringen vil bli klarere hvis vi vurderer den med et spesifikt eksempel (se figur).
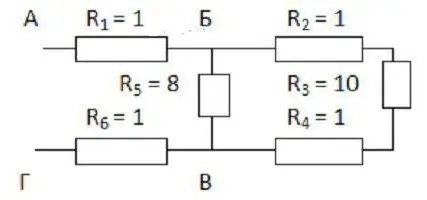
Det er praktisk å begynne å tegne fra punktene B og C. De må plasseres i en viss avstand fra hverandre og fra kantene på arket. På venstre side nærmer en ledning punkt B, og to er allerede rettet mot høyre. Punkt B har derimot to grener til venstre, og en ledning etter.
Nå må du fylle mellomrommet mellom disseprikker. Tre motstander med koeffisienter på 2, 3 og 4 bør plasseres langs den øverste ledningen, og den med en indeks på 5 vil gå fra bunnen. De tre første er koblet i serie. Med den femte motstanden er de parallelle.
De resterende to motstandene (den første og sjette) er koblet i serie med den betraktede delen av BV. Derfor kan tegningen ganske enkelt suppleres med to rektangler på hver side av de valgte punktene. Det gjenstår å bruke formlene for å beregne motstanden:
- først den som ble gitt for seriell tilkobling;
- da for parallell;
- og igjen for påfølgende.
På denne måten kan du distribuere et hvilket som helst, til og med svært komplisert opplegg.
Problemet med seriekobling av ledere
Tilstand. To lamper og en motstand er koblet i en krets bak hverandre. Den totale spenningen er 110 V og strømmen er 12 A. Hva er verdien av motstanden hvis hver lampe er vurdert til 40 V?
Beslutning. Siden en serieforbindelse vurderes, er formlene for dens lover kjent. Du trenger bare å bruke dem riktig. Start med å finne ut spenningsverdien over motstanden. For å gjøre dette må du trekke to ganger spenningen til en lampe fra totalen. Det viser seg 30 V.
Nå som to størrelser er kjent, U og I (den andre av dem er gitt i betingelsen, siden totalstrømmen er lik strømmen i hver serieforbruker), kan vi beregne motstanden til motstanden ved å bruke Ohms lov. Det viser seg å være 2,5 ohm.
Svar. Motstanden til motstanden er 2,5 ohm.
Oppgavefor tilkobling av kondensatorer, parallell og serie
Tilstand. Det er tre kondensatorer med kapasiteter på 20, 25 og 30 mikrofarad. Bestem deres totale kapasitans når koblet i serie og parallell.
Beslutning. Det er lettere å starte med en parallellkobling. I denne situasjonen må alle tre verdiene bare legges til. Dermed er den totale kapasitansen 75uF.
Beregningene blir noe mer kompliserte når disse kondensatorene kobles i serie. Tross alt, først må du finne forholdet mellom enhet til hver av disse kapasitetene, og deretter legge dem til hverandre. Det viser seg at enheten delt på totalkapasiteten er 37/300. Da er ønsket verdi omtrent 8 mikrofarader.
Svar. Den totale kapasitansen i seriekobling er 8 uF, parallelt - 75 uF.






