Elastisitetsmodul er en fysisk størrelse som karakteriserer den elastiske oppførselen til et materiale når en ytre kraft påføres det i en bestemt retning. Den elastiske oppførselen til et materiale betyr dets deformasjon i det elastiske området.
Historie om studiet av materialers elastisitet

Den fysiske teorien om elastiske kropper og deres oppførsel under påvirkning av ytre krefter ble vurdert i detalj og studert av den engelske vitenskapsmannen på 1800-tallet, Thomas Young. Selve begrepet elastisitet ble imidlertid utviklet tilbake i 1727 av den sveitsiske matematikeren, fysikeren og filosofen Leonhard Euler, og de første eksperimentene knyttet til elastisitetsmodulen ble utført i 1782, det vil si 25 år før arbeidet til Thomas Jung., av den venetianske matematikeren og filosofen Jacopo Ricatti.
Thomas Youngs fortjeneste ligger i det faktum at han ga elastisitetsteorien et slankt moderne utseende, som senere ble formalisert i form av en enkel og deretter generalisert Hookes lov.
Elastisitetens fysiske natur
Enhver kropp består av atomer, mellom hvilke kreftene tiltrekning og frastøting virker. Balansen mellom disse kreftene ermateriens tilstand og parametere under gitte forhold. Atomene i et fast legeme, når ubetydelige ytre spennings- eller kompresjonskrefter påføres dem, begynner å forskyve seg, og skaper en kraft i motsatt retning og lik størrelse, som har en tendens til å returnere atomene til sin opprinnelige tilstand.
I prosessen med en slik forskyvning av atomer, øker energien til hele systemet. Eksperimenter viser at ved små tøyninger er energien proporsjonal med kvadratet av disse tøyningene. Dette betyr at kraften, som er en derivativ med hensyn til energi, viser seg å være proporsjonal med den første kraften til tøyningen, det vil si at den avhenger lineært av den. Ved å svare på spørsmålet, hva er elastisitetsmodulen, kan vi si at dette er proporsjonalitetskoeffisienten mellom kraften som virker på atomet og deformasjonen som denne kraften forårsaker. Dimensjonen til Youngs modul er den samme som dimensjonen til trykk (Pascal).
Elastisk grense
I henhold til definisjonen indikerer elastisitetsmodulen hvor mye spenning som må påføres et fast stoff for at deformasjonen skal være 100 %. Imidlertid har alle faste stoffer en elastisk grense lik 1 % tøyning. Dette betyr at hvis en passende kraft påføres og kroppen deformeres med en mengde mindre enn 1 %, gjenoppretter kroppen nøyaktig sin opprinnelige form og dimensjoner etter avslutningen av denne kraften. Hvis det påføres for mye kraft, hvor deformasjonsverdien overstiger 1 %, etter avslutningen av den ytre kraften, vil kroppen ikke lenger gjenopprette sine opprinnelige dimensjoner. I det siste tilfellet snakker man om eksistensen av en gjenværende deformasjon, som erbevis på at elastisitetsgrensen for materialet er overskredet.
Youngs modul i aksjon
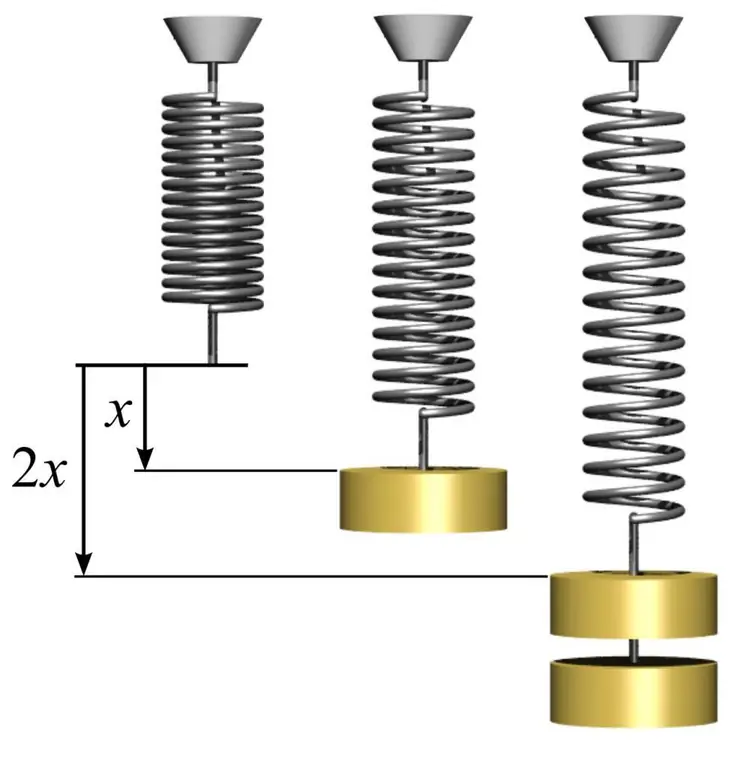
For å bestemme elastisitetsmodulen, samt for å forstå hvordan du bruker den, kan du gi et enkelt eksempel med en fjær. For å gjøre dette må du ta en metallfjær og måle arealet av sirkelen som spolene danner. Dette gjøres ved å bruke den enkle formelen S=πr², hvor n er pi lik 3,14 og r er radiusen til fjærens spole.
Deretter måler du lengden på fjæren l0 uten belastning. Hvis du henger en last med masse m1 på en fjær, vil den øke lengden til en viss verdi l1. Elastisitetsmodulen E kan beregnes basert på kunnskapen om Hookes lov ved hjelp av formelen: E=m1gl0/(S(l) 1-l0)), hvor g er akselerasjonen for fritt fall. I dette tilfellet legger vi merke til at mengden av deformasjon av fjæren i det elastiske området kan langt overstige 1%.
Å kjenne til Youngs modul gjør at du kan forutsi mengden deformasjon under påvirkning av en bestemt stress. I dette tilfellet, hvis vi henger en annen masse m2 på fjæren, får vi følgende verdi av relativ deformasjon: d=m2g/ (SE), hvor d - relativ deformasjon i det elastiske området.
Isotropi og anisotropi
Elastisitetsmodul er en egenskap ved et materiale som beskriver styrken til bindingen mellom dets atomer og molekyler, men et bestemt materiale kan ha flere forskjellige Youngs moduler.
Faktum er at egenskapene til hvert fast stoff avhenger av dens indre struktur. Hvis egenskapene er like i alle romlige retninger, så snakker vi om et isotropt materiale. Slike stoffer har en homogen struktur, så virkningen av en ekstern kraft i forskjellige retninger på dem forårsaker den samme reaksjonen fra materialet. Alle amorfe materialer er isotrope, som gummi eller glass.
Anisotropi er et fenomen som er preget av avhengigheten av de fysiske egenskapene til et fast stoff eller væske av retning. Alle metaller og legeringer basert på dem har et eller annet krystallgitter, det vil si et ordnet, snarere enn et kaotisk arrangement av ioniske kjerner. For slike materialer varierer elastisitetsmodulen avhengig av virkningsaksen til den ytre spenningen. For eksempel har metaller med kubisk symmetri, som aluminium, kobber, sølv, ildfaste metaller og andre, tre forskjellige Young-moduler.
Skjærmodul
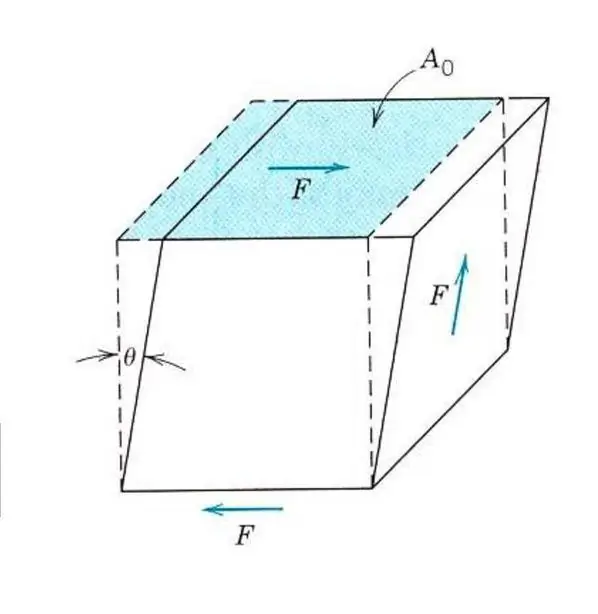
Beskrivelse av de elastiske egenskapene til selv et isotropt materiale krever ikke kunnskap om en Youngs modul. For i tillegg til strekk og kompresjon kan materialet påvirkes av skjærspenninger eller torsjonsspenninger. I dette tilfellet vil den reagere annerledes på ytre kraft. For å beskrive elastisk skjærdeformasjon introduseres en analog av Youngs modul, skjærmodul eller elastisitetsmodul av den andre typen.
Alle materialer motstår skjærspenninger mindre enn strekk eller kompresjon, så skjærmodulverdien for dem er 2-3 ganger mindre enn verdien av Youngs modul. For titan, hvis Youngs modul er lik 107 GPa, er skjærmodulenbare 40 GPa, for stål er disse tallene henholdsvis 210 GPa og 80 GPa.
Elastisitetsmodul for tre

Tre er et anisotropt materiale fordi trefibre er orientert i en bestemt retning. Det er langs fibrene at elastisitetsmodulen til tre måles, siden den er 1-2 størrelsesordener mindre over fibrene. Kunnskap om Youngs modul for tre er viktig og tas i betraktning ved utforming av trepanelkonstruksjoner.
Verdiene for elastisitetsmodulen til tre for noen typer trær er vist i tabellen nedenfor.
| Trevisning | Youngs modul i GPa |
| Laurbærtree | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Oak | 12 |
Det bør bemerkes at verdiene som er gitt kan variere med opptil 1 GPa for et bestemt tre, siden dets Young's modulus påvirkes av tettheten til treet og vekstforholdene.

Skjærmoduler for ulike treslag ligger i området 1-2 GPa, for eksempel for furu er det 1,21 GPa, og for eik 1,38 GPa, det vil si at trevirke praktisk t alt ikke motstår skjærpåkjenninger. Dette faktum må tas i betraktning ved fremstilling av bærende trekonstruksjoner, som er konstruert for kun å fungere i strekk eller kompresjon.
Elastiske egenskaper til metaller
Sammenlignet med Youngs tremodul, er gjennomsnittsverdiene for denne verdien for metaller og legeringer en størrelsesorden større, som vist i følgende tabell.
| Metal | Youngs modul i GPa |
| Bronse | 120 |
| Copper | 110 |
| Stål | 210 |
| Titanium | 107 |
| Nikkel | 204 |
Elastiske egenskaper til metaller som har en kubisk syngoni er beskrevet av tre elastiske konstanter. Slike metaller inkluderer kobber, nikkel, aluminium, jern. Hvis et metall har en sekskantet syngoni, trengs det allerede seks konstanter for å beskrive dets elastiske egenskaper.
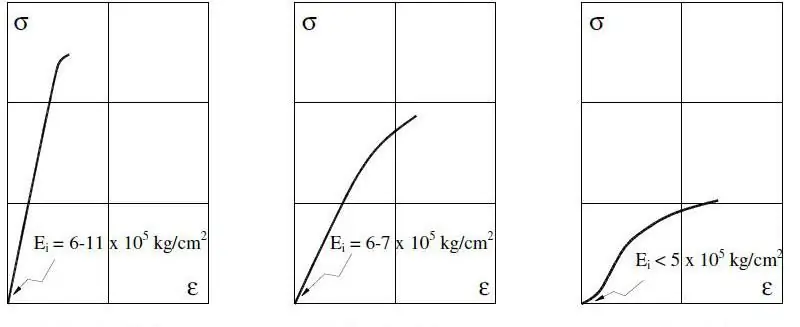
For metalliske systemer måles Youngs modul innenfor 0,2 % tøyning, da store verdier allerede kan forekomme i det uelastiske området.






