Pyramid sammen med et prisme er et perfekt polyeder i tredimensjon alt rom, deres geometriske egenskaper studeres på videregående. I denne artikkelen skal vi vurdere hva pyramider er, hvilke elementer de består av, og også kort karakterisere de riktige pyramidene.
Geometrisk figurpyramide
Fra et geometrisk synspunkt er pyramiden en romlig figur som består av en polygon og flere trekanter. Å få denne figuren er ganske enkelt. For å gjøre dette, ta en polygon med n sider, velg deretter et vilkårlig punkt i rommet som ikke vil ligge i polygonets plan, og koble hvert toppunkt i polygonet til dette punktet. Tydeligvis vil figuren som er dannet på denne måten ha n trekanter koblet til hverandre i ett toppunkt.
For å visualisere den geometriske formen til den beskrevne figuren, la oss ta et bilde.

Dette viser en firkantet pyramide, hvis base erfirkant, og sideflaten er dannet av fire trekanter som har et felles toppunkt.
Pyramidelementer
Pyramiden er som ethvert polyeder dannet av tre typer elementer:
- edges;
- tops;
- ribs.
Ansikter er deler av fly som skiller det indre volumet til en figur fra det omkringliggende rommet. Hvis bunnen av pyramiden inneholder en n-gon, er antallet flater alltid n+1. Av disse er n sider trekantede og en side er den nevnte n-gonale basen.
Høydepunkter er punkter der tre eller flere ansikter av en figur krysser hverandre. Baseområdet inneholder n toppunkter, som hver er dannet av to trekantede flater og en base. Punktet der n trekantede sider møtes kalles toppen av pyramiden. Dermed består figuren som vurderes av n+1 toppunkter.
Kanter er rette linjer som vises når to ansikter krysser hverandre. Hver kant er avgrenset av to toppunkter i endene. Enhver pyramide med en n-gon base inneholder 2n kanter. Halvparten av dette tallet, det vil si n, dannes utelukkende av skjæringspunktet mellom sidetrekanter.
Mulige typer figurer
Navnet på figuren som vurderes er unikt bestemt av typen polygon ved bunnen. For eksempel, hvis den har tre hjørner og tre sider, vil pyramiden være trekantet, hvis fire - firkantet, og så videre.
Polygon kan være konveks og konkav, i tillegg til vanlig og generell type. Alt dette bestemmer også pyramidens utseende.
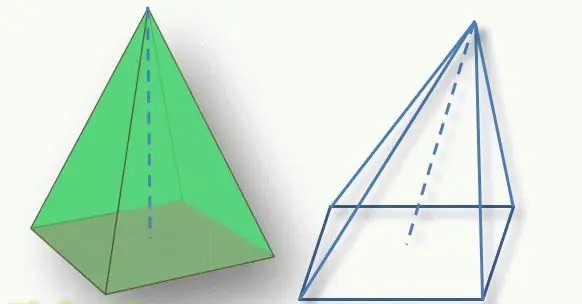
Et viktig poeng for å bestemme typen figur er plasseringen av toppen av pyramiden i forhold til basen. Det vinkelrette segmentet trukket fra toppen til den polygonale basen kalles høyden på figuren. Hvis dette segmentet skjærer basen ved dets geometriske sentrum (for en trekant er dette skjæringspunktet mellom medianer, for en firkant skjæringspunktet mellom diagonaler), kalles figuren en rett linje. Ellers snakker de om en skrå pyramide.
Hvis n-gonen til basen er regulær (likesidet trekant, firkant, etc.), og figuren er rett, kalles den en regulær pyramide.
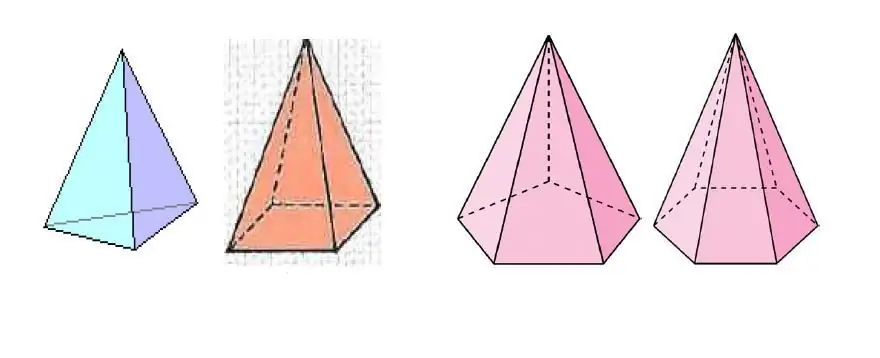
Bildet over viser flere pyramider, som er forskjellige i antall sider av polygonen ved bunnen.
Egenskaper til vanlige pyramider
Disse pyramidene skiller seg fra andre figurer i denne klassen ved en høy grad av symmetri. I denne forbindelse er det praktisk å utføre ulike geometriske beregninger med dem, for eksempel volum eller overflateareal.
En vanlig pyramide inneholder en n-gon ved bunnen, hvis areal er unikt bestemt ut fra kunnskapen om lengden på siden. Den laterale overflaten av figuren er dannet av n identiske trekanter, som er likesidede. Kantene på en vanlig pyramide på sideoverflaten er like med hverandre. Verdien av lengden på denne kanten brukes ofte når man beregner apotemet til en figur og bestemmer overflaten.
Høyden på en vanlig pyramide er den andre viktige egenskapen til figuren (den første er lengden på kantenbegrunnelse). Høyde brukes ved beregning av volum.
Ethvert plan parallelt med basen, som skjærer sideflatene til pyramiden, fører til dannelsen av en polygonal seksjon. Det er homotetisk med hensyn til basispolygonet. Den beskrevne skiveoperasjonen fører til dannelsen av en hel klasse med nye figurer - avkortede vanlige pyramider.
De mest kjente pyramidene

Selvfølgelig er dette de vanlige firkantede pyramidene til de egyptiske faraoene. På et sted som heter Giza, er det mer enn 100 av disse steinmonumentene, perfektion av design og nøyaktigheten til de geometriske parameterne som fortsetter å forbløffe forskere til i dag. Den største av dem er Keopspyramiden, som er omtrent 146 meter høy og omtrent 230 meter lang.
Hva nøyaktig disse pyramidene tjente til, samt hvilke mekanismer og når de ble bygget, vet ingen den dag i dag.






