For å kunne avbilde på papir gjenstander som i virkeligheten ikke har særlig "praktiske" størrelser, kom folk opp med en skala. Dette forklarer faktisk hva skalaen er til for.
Når skolens læreplan begynner å avsløre konseptet med skala
For første gang kommer barn over dette ordet mens de studerer kart og planer over området. Læreren forklarer hvorfor skalaen er nødvendig, hva den viser, ved å bruke atlas som eksempel. Det er forklart at ethvert geografisk trekk er så stort at det ville være vanskelig og upraktisk å skildre det i full størrelse.
Folk tegnet terrenget i redusert form, men til dette brukte de ingen eksakte forholdstall. Nå gjøres det smartere - hver strek og linje avbildet på kartet har en størrelse som kan multipliseres med et visst tall og finne ut den sanne lengden og bredden.
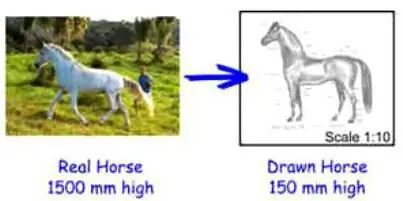
Rekordskala: den første måten å lese
Skalaen er indikert med to tall atskilt med et kolon. Det første sifferet angir dimensjonsenhetene i figuren, det andreangir hvor mange reelle enheter i figuren som tilsvarer det første tallet. For eksempel, hvis en skala på 1:1000 er angitt på en plan, og dimensjonsenhetene er angitt i centimeter, tilsvarer en centimeter i figuren 1000 cm i virkeligheten. Så hva er skalaen til? Med dens hjelp kan du ikke bare redusere enkelte objekter på den grafiske planen, men også nøyaktig beregne deres virkelige størrelse.
Den andre måten å ta opp skalaen på: hva er praktisk?
Den forrige metoden for å skrive skalaen gjennom et kolon kalles numerisk. Men det er også en navngitt skala. Rekorden hans er som følger: 1 cm - 20 km. Det viser seg at på denne måten er det mulig å kompakt skrive ned enorme skalaer som ikke vil bli uttrykt med tall med flere nuller, hvis det har oppstått en situasjon når det er nødvendig å indikere flere hundre kilometer på en centimeter. Samtidig er det umiddelbart klart hvor mye, hva og i hva. Denne posten er mer intuitiv og tydelig.
Skalering i tegning: hva utfyller det tidligere studerte konseptet
Begrepet skala møter vi ikke bare i geografi, men også i studiet av et slikt emne som tegning. De samme prinsippene brukes til å skildre ulike objekter. Men det er en vesentlig forskjell: her utvides også begrepet hva skala er for ved at det kan brukes til å avbilde små detaljer i større skala. I geografi snakker vi ikke om dette, for det er ikke så små objekter i geografien at det er behov for å forstørre dem. Kontinenter og fjell, elver og innsjøer er i alle fall større enn ark med A4-papir eller til og medA1.
Når du studerer tegning, kan du bruke skalaen til å avbilde de minste detaljene i større form, for eksempel en bolt eller tannhjul.
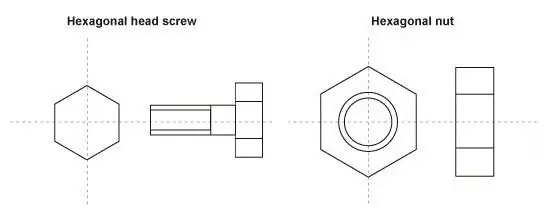
Så hvorfor trenger vi en skala i dette tilfellet? Med dens hjelp kan du mer praktisk, tydelig og detaljert skildre et lite element. I dette tilfellet skjer det motsatte i notasjonen: det første tallet vil være større enn det andre, og notasjonen 100:1 vil høres omtrent slik ut: 100 metriske enheter av bildet tilsvarer én enhet av den faktiske størrelsen.
Noen oppklarende eksempler
Hva er skalaen for, hva viser den i tilfelle et bilde av en mindre gjenstand, som er resultatet på papir? Igjen har vi det nøyaktige forholdet mellom dimensjonene til bildet av delen og det virkelige objektet. Husk den samme skalaen på 100:1. Det viser seg at i hundre millimeter i figuren er det bare én millimeter reell størrelse. Hvis en del er 500 millimeter bred på bildet, er dens faktiske bredde bare 5 millimeter.
Hvis vi husker det første tilfellet, bildet på et ark av en mindre kopi av et stort objekt, vil skalaen 1:100 bety at en millimeter i bildet inneholder 100 millimeter av den sanne størrelsen. Så hvis et objekt er 80 millimeter langt på en tegning eller kart, vil den faktiske lengden på objektet være 8000 millimeter. Et tydelig eksempel på hva målestokk er for og hvilken praktisk oppfinnelse av menneskeheten.
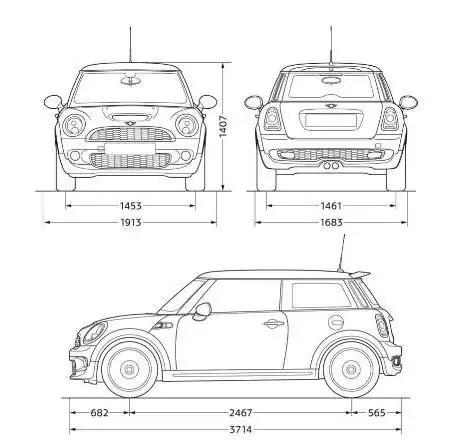
Det viktigste med å bruke skalaen er umiddelbarthusk at det første tallet refererer til bildet og det andre til den faktiske størrelsen på objektene. For ikke å bli forvirret i fremtiden, for å konsolidere disse grunnlagene, holdes praktiske klasser i geografi på skolene slik at barn forklarer og beregner størrelsen på virkelige objekter flere ganger ved hjelp av atlaset. Det samme skjer i tegnetimer.
Sumarize
Hva er skalaen til? Svaret på dette spørsmålet består av tre punkter som du bare trenger å huske:
- Først - skalaen er nødvendig for å vise store objekter på en overflate som er praktisk å se.
- Second - skalaen er nødvendig for å avbilde små objekter i større størrelse.
- Tredje - skalaen er nødvendig for å kunne bestemme størrelsen på et ekte objekt nøyaktig, uavhengig av dens opprinnelige størrelse, liten eller stor.






