Når fagfellevurdering, for eksempel, vurderer produkters konkurranseevne, er det nødvendig, som i ethvert vitenskapelig arbeid, å gjennomføre statistisk databehandling. Sistnevnte begynner med å bestemme konsistensen av ekspertuttalelser, hvis numeriske uttrykk er konkordanskoeffisienten.
Hvorfor trenger vi en ekspertkonsensusvurdering?
Denne vurderingen er først og fremst nødvendig fordi ekspertenes meninger kan variere sterkt når det gjelder estimerte parametere. Til å begynne med utføres vurderingen ved å rangere indikatorene og tildele dem en viss betydningskoeffisient (vekt). En inkonsekvent rangering resulterer i at disse koeffisientene er statistisk upålitelige. Uttalelsene til eksperter med det nødvendige antallet (mer enn 7-10) bør distribueres i henhold til vanlig lov.
Konseptet med konkordansskoeffisienten
Så. Konsistens er konkordans. Koeffisienten er en dimensjonsløs mengde som viser forholdet mellom dispersjonen og den maksimale dispersjonen i det generelle tilfellet. La oss generalisere disse begrepene.
Konkordansskoeffisient er et tall fra 0 til 1, som viser konsistensen av ekspertuttalelser nårrangering av noen eiendommer. Jo nærmere denne verdien er 0, jo lavere blir konsistensen vurdert. Hvis verdien av denne koeffisienten er mindre enn 0,3, anses ekspertenes meninger som inkonsekvente. Når verdien av koeffisienten er i området fra 0,3 til 0,7, anses konsistensen som gjennomsnittlig. En verdi større enn 0,7 anses som høy konsistens.
Use cases
Når man utfører statistiske undersøkelser, kan det oppstå situasjoner der et objekt ikke kan karakteriseres av to sekvenser, som er statistisk behandlet ved hjelp av konkordanskoeffisienten, men av flere sekvenser, som følgelig er rangert av eksperter med samme nivå av profesjonalitet på et bestemt område.
Konsistensen i rangeringen utført av eksperter må bestemmes for å bekrefte riktigheten av hypotesen om at eksperter gjør relativt nøyaktige målinger, noe som gjør det mulig å danne ulike grupperinger i ekspertgrupper, som i stor grad bestemmes av menneskelige faktorer, primært som forskjeller i synspunkter, konsepter, ulike vitenskapelige skoler, arten av profesjonell aktivitet, etc.
Kort beskrivelse av rangeringsmetoden. Dens fordeler og ulemper
Ved rangering brukes rangeringsmetoden. Dens essens ligger i det faktum at hver egenskap til objektet er tildelt sin egen spesifikke rangering. Dessuten er hver ekspert som er inkludert i ekspertgruppen, denne rangeringen tildeltuavhengig, noe som resulterer i behovet for å behandle disse dataene for å identifisere konsistensen i ekspertuttalelser. Denne prosessen utføres ved å beregne konkordansskoeffisienten.
Den største fordelen med rangeringsmetoden er dens enkle implementering.
De viktigste ulempene med metoden er:
- et lite antall rangeringsobjekter, siden når antallet overstiger 15-20, blir det vanskelig å tildele objektive rangeringspoeng;
- Basert på bruken av denne metoden forblir spørsmålet om hvor langt de studerte objektene er fra hverandre i betydning åpent.
Når du bruker denne metoden, må det tas i betraktning at vurderingene er basert på en slags sannsynlighetsmodell, så de må brukes med forsiktighet, gitt omfanget.
Kendall's Concordance Rank Coefficient
Brukes for å bestemme forholdet mellom kvantitative og kvalitative trekk som karakteriserer homogene objekter og rangert etter samme prinsipp.
Denne koeffisienten bestemmes av formelen:
t=2S/(n(n-1)), hvor
S - summen av forskjellene mellom antall sekvenser og antall inversjoner på den andre funksjonen;
n - antall observasjoner.

Beregningsalgoritme:
- X-verdiene er rangert i stigende eller synkende rekkefølge.
- Y-verdiene er ordnet i den rekkefølgen de tilsvarer x-verdiene.
- For hver påfølgende rangering av y, avgjør hvor mange høyere rangeringsverdier som følger den. De legges sammen, og korrespondansemålet for rekkefølger i x og y beregnes.
- Tilsvarende beregnes antall rangeringer av y med lavere verdier, som også summeres.
- Legg til antall rangeringer med høyere verdier og antall rangeringer med lavere verdier, noe som resulterer i verdien S.
Denne koeffisienten viser forholdet mellom to variabler, og kalles i de fleste tilfeller Kendall-rangkorrelasjonskoeffisienten. Slik avhengighet kan representeres grafisk.
Fastsetting av koeffisient
Hvordan gjøres det? Hvis antallet rangerte funksjoner eller faktorer overstiger 2, brukes konkordanskoeffisienten, som i hovedsak er en multippel variant av rangkorrelasjon.
Vær forsiktig. Beregningen av konkordanskoeffisienten er basert på forholdet mellom avviket av summen av kvadrater av ranger fra den gjennomsnittlige summen av kvadrater av ranger, multiplisert med 12, til kvadratet av eksperter, multiplisert med forskjellen mellom kuben av tallet av objekter og antall objekter.
Beregningsalgoritme
For å forstå hvor tallet 12 kommer fra i telleren til beregningsformelen, la oss se på bestemmelsesalgoritmen.
For hver linje med gradene til en bestemt ekspert, beregnes summen av gradene, som er en tilfeldig verdi.
Konkordanskoeffisienten er generelt definert som forholdet mellom variansestimatet (D) og maksimalverdien av variansestimatet(Dmax). La oss suksessivt formulere definisjonene av disse mengdene.
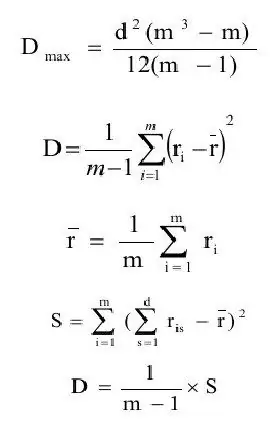
hvor ravg - forventningsestimat;
m - antall objekter.
Ved å erstatte de resulterende formlene i forhold til D med Dmax får vi den endelige formelen for konkordanskoeffisienten:
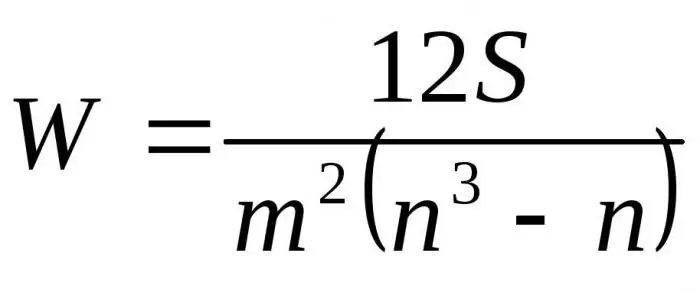
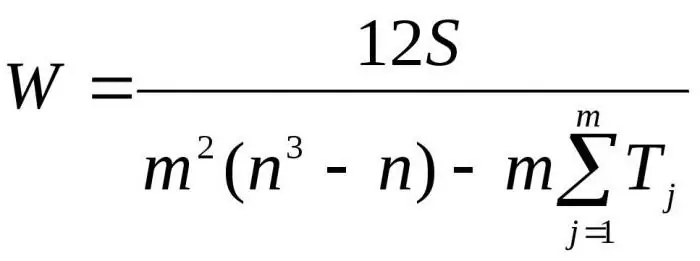
Her er m antall eksperter, n er antall objekter.
Den første formelen brukes til å bestemme konkordansfaktoren hvis det ikke er relaterte rangeringer. Den andre formelen brukes hvis det er relaterte rangeringer.
Så, beregningen av konkordanskoeffisienten er over. Hva blir det neste? Den oppnådde verdien evalueres for signifikans ved å bruke Pearson-koeffisienten ved å multiplisere denne koeffisienten med antall eksperter og med antall frihetsgrader (m-1). Det resulterende kriteriet sammenlignes med tabellverdien, og hvis verdien av den første overstiger den siste, snakker de om betydningen av koeffisienten som studeres.
Når det gjelder relaterte rangeringer, blir beregningen av Pearson-kriteriet noe mer komplisert og utføres med følgende forhold: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Eksempel
Anta at ekspertmetoden vurderer konkurranseevnen til smør som selges i et detaljhandelsnettverk. La oss gi et eksempel på beregning av konkordanskoeffisienten. Før man vurderer konkurranseevnen, er det nødvendig å rangere forbrukerenegenskaper ved dette produktet som er involvert i evalueringen. La oss anta at disse egenskapene vil være følgende: smak og lukt, konsistens og utseende, farge, emballasje og merking, fettinnhold, handelsnavn, produsent, pris.
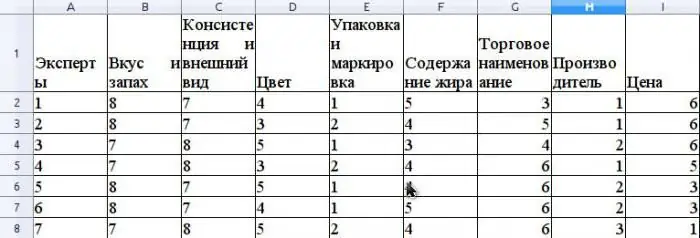
Anta at ekspertgruppen består av 7 eksperter. Figuren viser resultatene av rangeringen av disse egenskapene.
Gjennomsnittsverdien av r beregnes som det aritmetiske gjennomsnittet og vil være 31,5. For å finne S, summerer du kvadrerte forskjeller mellom ris og r gjennomsnitt, i henhold til formelen ovenfor, og fastslå at verdien av S er 1718.
Beregn konkordanskoeffisienten ved å bruke formelen uten å bruke relaterte rangeringer (rangeringer ville vært relatert hvis den samme ekspertrådgiveren hadde samme rangeringer for forskjellige egenskaper).
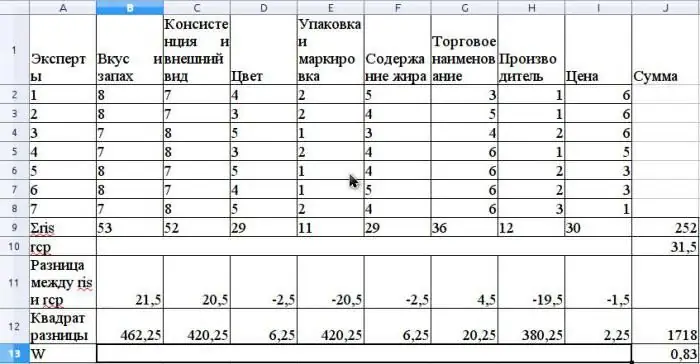
Verdien av denne koeffisienten vil være 0,83. Dette indikerer en sterk konsensus blant eksperter.
Sjekk dens betydning ved å bruke Pearson-testen:
7 x 0,83 x (8-1)=40,7.
Pearsons tabelltest ved 1 % signifikansnivå er 18,5, og ved 5 % - 14,1..
Eksemplet demonstrerer enkelheten og tilgjengeligheten til beregningen for enhver person som kan det grunnleggende om matematiske beregninger. For å lindre dem,bruk regnearkskjemaer.
Til avslutning
Dermed viser konkordansskoeffisienten konsistensen i flere eksperters meninger. Jo lenger det er fra 0 og nærmere 1, jo mer konsistente meninger. Disse koeffisientene må bekreftes ved å beregne Pearson-kriteriet.






