Oppløsning er et bildesystems evne til å reprodusere detaljene til et objekt, og avhenger av faktorer som typen belysning som brukes, pikselstørrelsen til sensoren og optikkens muligheter. Jo mindre detalj på motivet, desto høyere er den nødvendige oppløsningen til objektivet.
Introduksjon til løsningsprosessen
Bildekvaliteten til kameraet avhenger av sensoren. Enkelt sagt er en digital bildesensor en brikke inne i et kamerahus som inneholder millioner av lysfølsomme flekker. Størrelsen på kameraets sensor avgjør hvor mye lys som kan brukes til å lage et bilde. Jo større sensor, desto bedre bildekvalitet ettersom mer informasjon samles inn. Vanligvis annonserer digitale kameraer i markedet for sensorstørrelser på 16 mm, Super 35 mm og noen ganger opptil 65 mm.
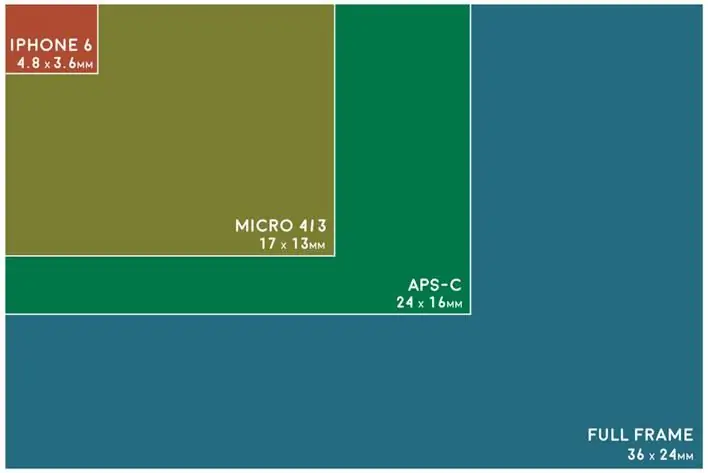
Når størrelsen på sensoren øker, vil dybdeskarpheten avta ved en gitt blenderåpning, da en større motpart krever at du kommer nærmereobjekt eller bruk en lengre brennvidde for å fylle rammen. For å opprettholde samme dybdeskarphet må fotografen bruke mindre blenderåpninger.
Denne grunne dybdeskarpheten kan være ønskelig, spesielt for å oppnå bakgrunnsuskarphet for portretter, men landskapsfotografering krever mer dybde, noe som er lettere å fange med den fleksible blenderåpningen til kompaktkameraer.
Deling av antall horisontale eller vertikale piksler på en sensor vil indikere hvor mye plass hver enkelt opptar på et objekt, og kan brukes til å evaluere objektivets løsningsevne og løse kundenes bekymringer om enhetens digitale bildepikselstørrelse. Som et utgangspunkt er det viktig å forstå hva som faktisk kan begrense systemets oppløsning.
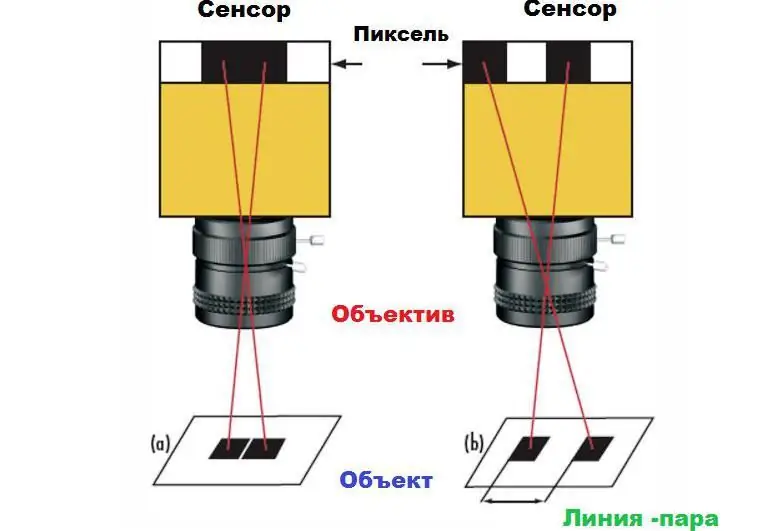
Dette utsagnet kan demonstreres med eksempelet med et par firkanter på en hvit bakgrunn. Hvis firkantene på kamerasensoren er kartlagt til nabopiksler, vil de vises som ett stort rektangel i bildet (1a) i stedet for to separate firkanter (1b). For å skille rutene kreves det et visst mellomrom mellom dem, minst én piksel. Denne minste avstanden er den maksimale oppløsningen til systemet. Den absolutte grensen bestemmes av størrelsen på pikslene på sensoren, samt antallet deres.
Målelinseegenskaper
Forholdet mellom vekslende svarte og hvite firkanter beskrives som et lineært par. Vanligvis bestemmes oppløsningen av frekvensen,målt i linjepar per millimeter - lp/mm. Dessverre er objektivets oppløsning i cm ikke et absolutt tall. Ved en gitt oppløsning vil muligheten til å se de to rutene som separate objekter avhenge av gråskalanivået. Jo større gråskala-separasjon mellom dem og rommet, jo mer stabil er evnen til å løse disse firkantene. Denne inndelingen av gråskalaen er kjent som frekvenskontrast.
Rolig frekvens er gitt i lp/mm. Av denne grunn er det ekstremt nyttig å beregne oppløsning i form av lp/mm når du sammenligner objektiver og bestemmer det beste valget for gitte sensorer og applikasjoner. Den første er der systemoppløsningsberegningen starter. Fra og med sensoren er det lettere å finne ut hvilke objektivspesifikasjoner som trengs for å oppfylle kravene til enheten eller andre applikasjoner. Den høyeste frekvensen tillatt av sensoren, Nyquist, er faktisk to piksler eller ett linjepar.
Definisjonslinseoppløsning, også k alt systembildeoppløsning, kan bestemmes ved å multiplisere størrelsen i Μm med 2 for å lage et par og dele på 1000 for å konvertere til mm:
lp/mm=1000/ (2 x piksler)
Sensorer med større piksler vil ha lavere oppløsningsgrenser. Sensorer med mindre piksler vil yte bedre i henhold til formelen for objektivoppløsning ovenfor.
Aktivt sensorområde
Du kan beregne maksimal oppløsning for objektetvisning. For å gjøre dette er det nødvendig å skille mellom indikatorer som forholdet mellom størrelsen på sensoren, synsfeltet og antall piksler på sensoren. Størrelsen på sistnevnte refererer til parameterne for det aktive området til kamerasensoren, vanligvis bestemt av størrelsen på formatet.
De nøyaktige proporsjonene vil imidlertid variere etter sideforhold, og nominelle sensorstørrelser bør kun brukes som en retningslinje, spesielt for telesentriske objektiver og høye forstørrelser. Sensorstørrelsen kan beregnes direkte fra pikselstørrelsen og det aktive antallet piksler for å utføre en objektivoppløsningstest.
Tabellen viser Nyquist-grensen knyttet til pikselstørrelser som finnes på noen svært vanlig brukte sensorer.
| Pikselstørrelse (µm) | Koblet Nyquist-grense (lp / mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
Når pikselstørrelsene reduseres, øker den tilhørende Nyquist-grensen i lp/mm proporsjon alt. For å bestemme det absolutt minste oppløselige punktet som kan sees på et objekt, må forholdet mellom synsfeltet og størrelsen på sensoren beregnes. Dette er også kjent som primær forstørrelse.(PMAG)-systemer.
Forholdet knyttet til systemet PMAG gjør det mulig å skalere bildeoppløsningen. Vanligvis, når du designer en applikasjon, er den ikke spesifisert i lp/mm, men snarere i mikron (µm) eller brøkdeler av en tomme. Du kan raskt hoppe til den ultimate oppløsningen til et objekt ved å bruke formelen ovenfor for å gjøre det enklere å velge objektivoppløsningen z. Det er også viktig å huske på at det er mange tilleggsfaktorer, og begrensningen ovenfor er mye mindre utsatt for feil enn kompleksiteten ved å ta hensyn til mange faktorer og beregne dem ved hjelp av ligninger.
Beregn brennvidde
Oppløsningen til et bilde er antall piksler i det. Utpekt i to dimensjoner, for eksempel 640X480. Beregninger kan gjøres separat for hver dimensjon, men for enkelhets skyld reduseres dette ofte til én. For å gjøre nøyaktige målinger på et bilde, må du bruke minimum to piksler for hvert minste område du vil oppdage. Størrelsen på sensoren refererer til en fysisk indikator og er som regel ikke angitt i passdataene. Den beste måten å bestemme størrelsen på en sensor på er å se på pikselparametrene på den og multiplisere den med sideforholdet, i så fall løser objektivets oppløsningsevne problemene med et dårlig skudd.
Basler acA1300-30um-kameraet har for eksempel en pikselstørrelse på 3,75 x 3,75 um og en oppløsning på 1296 x 966 piksler. Sensorstørrelsen er 3,75 µm x 1296 x 3,75 µm x 966=4,86 x 3,62 mm.
Sensorformat refererer til den fysiske størrelsen og er ikke avhengig av pikselstørrelsen. Denne innstillingen brukes tilfinne ut hvilket objektiv kameraet er kompatibelt med. For at de skal matche, må linseformatet være større enn eller lik sensorstørrelsen. Hvis et objektiv med et mindre sideforhold brukes, vil bildet oppleve vignettering. Dette fører til at områder av sensoren utenfor kanten av objektivformatet blir mørke.
Piksler og kameravalg

For å se objektene i bildet må det være nok plass mellom dem slik at de ikke smelter sammen med nabopiksler, ellers vil de ikke kunne skilles fra hverandre. Hvis objektene er en piksel hver, må separasjonen mellom dem også være minst ett element, det er takket være dette at det dannes et par linjer, som faktisk har to piksler i størrelse. Dette er en av grunnene til at det er feil å måle oppløsningen til kameraer og objektiver i megapiksler.
Det er faktisk lettere å beskrive oppløsningsmulighetene til et system når det gjelder linjeparfrekvens. Det følger at når pikselstørrelsen reduseres, øker oppløsningen fordi du kan plassere mindre objekter på mindre digitale elementer, ha mindre plass mellom dem, og fortsatt bestemme avstanden mellom motivene du fotograferer.
Dette er en forenklet modell av hvordan kameraets sensor oppdager objekter uten å ta hensyn til støy eller andre parametere, og er den ideelle situasjonen.
MTF-kontrastdiagrammer
De fleste linser er ikke perfekte optiske systemer. Lys som passerer gjennom en linse gjennomgår en viss grad av nedbrytning. Spørsmålet er hvordan man skal vurdere dettedegradering? Før du svarer på dette spørsmålet, er det nødvendig å definere konseptet "modulasjon". Sistnevnte er et mål på kontrasten len ved en gitt frekvens. Man kan prøve å analysere bilder fra den virkelige verden tatt gjennom en linse for å bestemme modulering eller kontrast for detaljer av forskjellige størrelser eller frekvenser (mellomrom), men dette er veldig upraktisk.
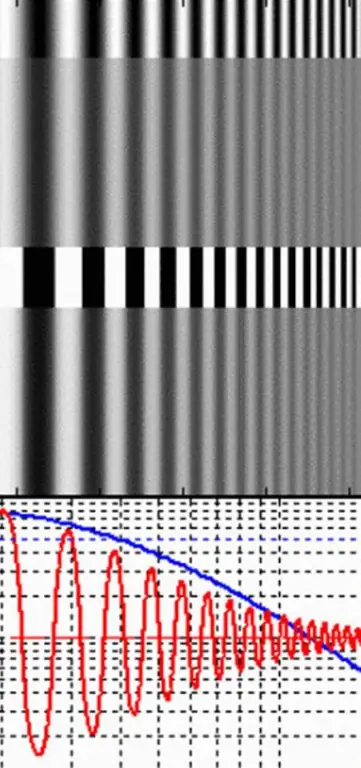
I stedet er det mye lettere å måle modulasjon eller kontrast for par med alternerende hvite og mørke linjer. De kalles rektangulært gitter. Intervallet av linjer i et rektangulært bølgegitter er frekvensen (v), for hvilken modulasjons- eller kontrastfunksjonen til linsen og oppløsningen måles i cm.
Maksimal mengde lys vil komme fra de lyse båndene, og minimum fra de mørke båndene. Hvis lys måles i lysstyrke (L), kan modulasjonen bestemmes i henhold til følgende ligning:
modulasjon=(Lmax - Lmin) / (Lmax + Lmin), hvor: Lmax er maksimal lysstyrke for hvite linjer i gitteret, og Lmin er minimum lysstyrke for mørke.
Når modulasjon er definert i form av lys, blir det ofte referert til som Michelson-kontrast fordi det tar forholdet mellom luminans fra lyse og mørke bånd for å måle kontrast.
For eksempel er det et firkantbølgegitter med en viss frekvens (v) og modulasjon, og en iboende kontrast mellom mørke og lyse områder reflektert fra dette gitteret gjennom linsen. Bildemodulasjon og dermed linsekontrast måles for en gitt frekvenstakter (v).
Modulasjonsoverføringsfunksjonen (MTF) er definert som modulasjonen M i av bildet delt på modulasjonen av stimulusen (objektet) M o, som vist i følgende ligning.
|
MTF (v)=M i / M 0 |
USF-testnett er trykt på 98 % sterkt laserpapir. Svart laserskrivertoner har en reflektans på omtrent 10 %. Så verdien for M 0 er 88 %. Men siden film har et mer begrenset dynamisk område sammenlignet med det menneskelige øyet, er det trygt å anta at M 0 i hovedsak er 100 % eller 1. Så formelen ovenfor koker ned til følgende mer enkel ligning:
|
MTF (v)=Mi |
Så MTF-linsen for en gitt gitterfrekvens (v) er ganske enkelt den målte gittermodulasjonen (Mi) når det fotograferes gjennom en linse på film.
Mikroskopoppløsning
Oppløsningen til et mikroskopobjektiv er den korteste avstanden mellom to distinkte punkter i okularets synsfelt som fortsatt kan skilles ut som forskjellige objekter.
Hvis to punkter er nærmere hverandre enn oppløsningen din, vil de virke uklare og posisjonene deres vil være unøyaktige. Mikroskopet kan tilby høy forstørrelse, men hvis linsene er av dårlig kvalitet, vil den resulterende dårlige oppløsningen forringe bildekvaliteten.
Nedenfor er Abbe-ligningen, der oppløsningenkraften til et mikroskopobjektiv z er oppløsningskraften lik bølgelengden til lyset som brukes delt på 2 (den numeriske blenderåpningen til objektivet).
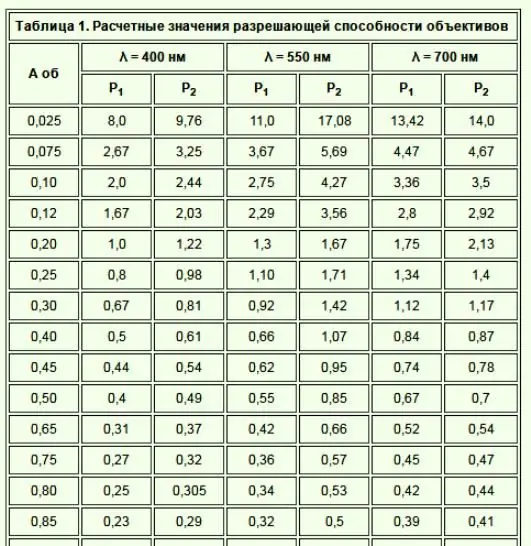
Flere elementer påvirker oppløsningen til et mikroskop. Et optisk mikroskop satt til høy forstørrelse kan produsere et bilde som er uskarpt, men det har fortsatt den maksimale oppløsningen til linsen.
Den digitale blenderåpningen til et objektiv påvirker oppløsningen. Oppløsningsevnen til et mikroskopobjektiv er et tall som indikerer evnen til en linse til å samle lys og løse opp et punkt i en fast avstand fra objektivet. Det minste punktet som kan løses opp av linsen er proporsjon alt med bølgelengden til det oppsamlede lyset delt på det numeriske blendertallet. Derfor tilsvarer et større antall en større evne til objektivet til å oppdage et utmerket punkt i synsfeltet. Den numeriske blenderåpningen til objektivet avhenger også av mengden optisk aberrasjonskorreksjon.
Opløsning av teleskoplinsen
Som en lystrakt er et teleskop i stand til å samle lys i forhold til arealet av hullet, denne egenskapen er hovedlinsen.
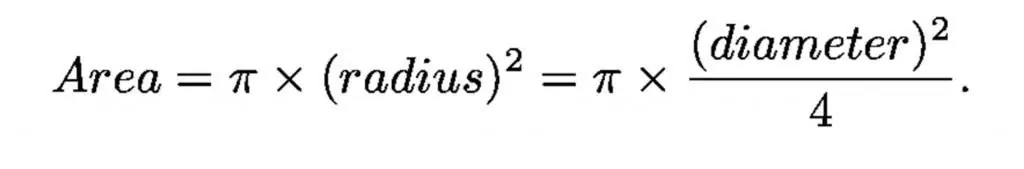
Diameteren på den mørke tilpassede pupillen til det menneskelige øyet er i underkant av 1 centimeter, og diameteren på det største optiske teleskopet er 1000 centimeter (10 meter), slik at det største teleskopet er en million ganger større i samlingen område enn det menneskelige øyet.

Dette er grunnen til at teleskoper ser svakere gjenstander enn mennesker. Og ha enheter som samler lys ved hjelp av elektroniske deteksjonssensorer i mange timer.
Det er to hovedtyper av teleskoper: linsebaserte refraktorer og speilbaserte reflektorer. Store teleskoper er reflektorer fordi speil ikke trenger å være gjennomsiktige. Teleskopspeil er blant de mest presise designene. Den tillatte feilen på overflaten er omtrent 1/1000 av bredden til et menneskehår - gjennom et 10 meter hull.
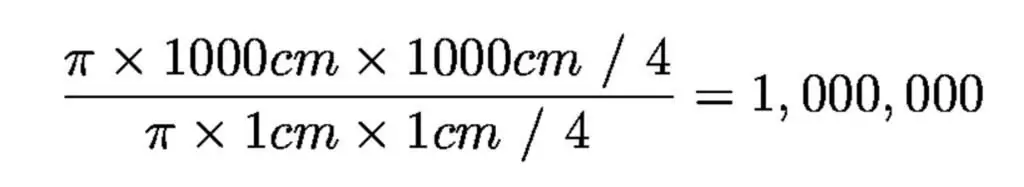
Speil pleide å være laget av enorme tykke glassplater for å hindre dem fra å henge. Dagens speil er tynne og fleksible, men er datastyrt eller på annen måte segmentert og justert av datakontroll. I tillegg til oppgaven med å finne svake gjenstander, er astronomens mål også å se de fine detaljene deres. Graden som detaljer kan gjenkjennes kalles oppløsning:
- Fuzzy bilder=dårlig oppløsning.
- Klare bilder=god oppløsning.
På grunn av bølgenaturen til lys og fenomener k alt diffraksjon, begrenser diameteren til et teleskops speil eller linse dens ultimate oppløsning i forhold til diameteren til teleskopet. Oppløsningen betyr her den minste vinkeldetaljen som kan gjenkjennes. Små verdier tilsvarer utmerket bildedetaljer.
Radioteleskoper må være veldig store for å gi god oppløsning. Jordens atmosfære erturbulente og uskarpe teleskopbilder. Terrestriske astronomer kan sjelden nå den maksimale oppløsningen til apparatet. Atmosfærens turbulente effekt på en stjerne kalles syn. Denne turbulensen får stjernene til å "glitre". For å unngå disse atmosfæriske uskarphetene sender astronomer ut teleskoper ut i verdensrommet eller plasserer dem på høye fjell med stabile atmosfæriske forhold.
Eksempler på parameterberegning
Data for å bestemme Canon-objektivets oppløsning:
- Pikselstørrelse=3,45 µm x 3,45 µm.
- piksler (H x V)=2448 x 2050.
- Ønsket synsfelt (horisont alt)=100 mm.
- Sensoroppløsningsgrense: 1000/2x3, 45=145 lp / mm.
- Sensordimensjoner:3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Målelinseoppløsning: 145 x 0,0845=12,25 lp/mm.
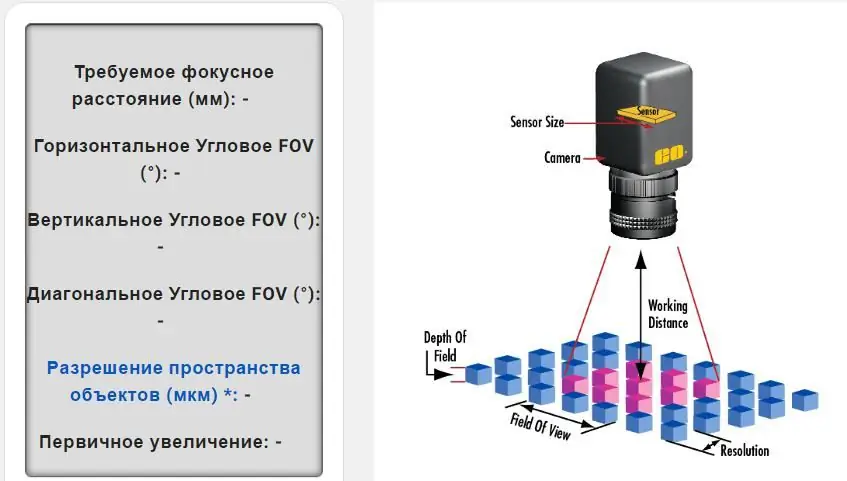
Egentlig er disse beregningene ganske komplekse, men de vil hjelpe deg med å lage et bilde basert på sensorstørrelse, pikselformat, arbeidsavstand og synsfelt i mm. Beregning av disse verdiene vil finne det beste objektivet for bildene og applikasjonen din.
Problemer med moderne optikk

Dessverre skaper dobling av størrelsen på sensoren ytterligere problemer for linser. En av hovedparametrene som påvirker kostnadene for et bildeobjektiv er formatet. Å designe et objektiv for en sensor i større format krevermange individuelle optiske komponenter, som bør være større og overføringen av systemet mer stiv.
Et objektiv designet for en 1"-sensor kan koste fem ganger så mye som et objektiv designet for en ½"-sensor, selv om det ikke kan bruke de samme spesifikasjonene med begrenset pikseloppløsning. Kostnadskomponenten må vurderes før hvordan for å bestemme oppløsningsevnen til en linse.
Optisk bildebehandling i dag står overfor flere utfordringer enn for et tiår siden. Sensorene de brukes med har mye høyere oppløsningskrav, og formatstørrelser drives samtidig både mindre og større, mens pikselstørrelsen fortsetter å krympe.
Tidligere begrenset aldri optikk bildebehandlingssystemet, i dag gjør det det. Der en typisk pikselstørrelse er rundt 9 µm, er en mye mer vanlig størrelse rundt 3 µm. Denne 81x økningen i punkttetthet har tatt sitt toll på optikken, og selv om de fleste enheter er gode, er objektivvalg nå viktigere enn noen gang.






