Det finnes alle slags mekaniske enheter. Noen av dem er kjent for oss fra barndommen. Dette er for eksempel klokker, sykler, snurrer. Vi lærer om andre når vi blir eldre. Dette er motorer til biler, vinsjer til kraner og andre. Hver bevegelig mekanisme bruker et slags system for å få hjulene til å snu og maskinen fungere. En av de mest interessante og populære er den planetariske mekanismen. Dens essens ligger i det faktum at maskinen drives av hjul eller tannhjul som samhandler med hverandre på en spesiell måte. La oss se nærmere på det.
Generell informasjon
Planetgiret og planetmekanismen heter slik i analogi med vårt solsystem, som kan betinget representeres som følger: i midten er det en "sol" (det sentrale hjulet i mekanismen). "Planeter" (små hjul eller satellitter) beveger seg rundt den. Alle disse delene i planetgiret har ytre tenner. Det betingede solsystemet har en grense i diameteren. Rolledet utføres i planetmekanismen av et stort hjul eller episykkel. Den har også tenner, kun interne. Det meste av arbeidet i denne designen utføres av bæreren, som er en spakmekanisme. Bevegelse kan utføres på forskjellige måter: enten vil solen rotere, eller episykkelen, men alltid sammen med satellittene.
Under driften av planetmekanismen kan en annen design brukes, for eksempel to soler, satellitter og en bærer, men uten episykkel. Et annet alternativ er to episykler, men uten sol. Transportør og satellitter må alltid være tilstede. Avhengig av antall hjul og plasseringen av deres rotasjonsakser i rommet, kan designet være enkelt eller komplekst, flatt eller romlig.
For å forstå hvordan et slikt system fungerer, må du forstå detaljene.
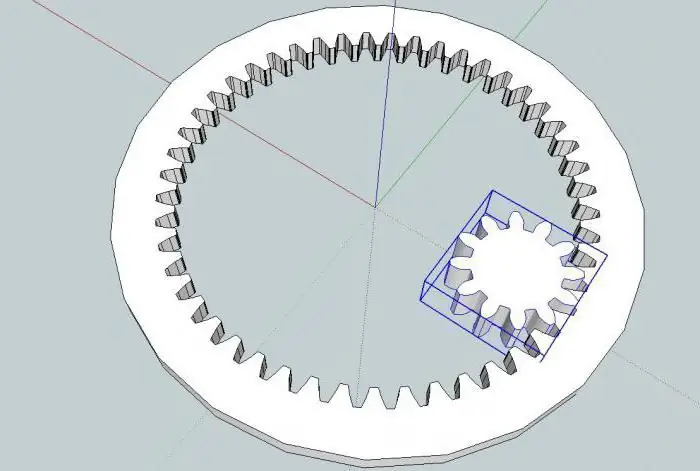
Plassering av elementer
Den enkleste formen for planetgir inkluderer tre sett med gir med varierende frihetsgrader. Satellittene ovenfor roterer rundt sine akser og samtidig rundt solen, som forblir på plass. Episykkelen forbinder planetmekanismen fra utsiden og roterer også ved hjelp av et alternativt inngrep av tennene (den og satellittene). Denne designen er i stand til å endre dreiemomentet (vinkelhastigheter) i ett plan.
I en enkel planetmekanisme kan solen og satellittene rotere, mens episenteret forblir fast. Uansett er vinkelhastighetene til alle komponentene ikke kaotiske, men har en lineær avhengighet av hverandre. Når mediet roterer, gir detlav hastighet høyt dreiemoment utgang.
Det vil si at essensen av planetgiret er at et slikt design er i stand til å endre, utvide og legge til dreiemoment og vinkelhastighet. Rotasjonsbevegelser i dette tilfellet skjer i en geometrisk akse. Det nødvendige transmisjonselementet til ulike kjøretøy og mekanismer er installert.

Funksjoner av strukturelle materialer og skjemaer
En fast komponent er imidlertid ikke alltid nødvendig. I differensialsystemer roterer hvert element. Planetgir som dette har én utgangsdrevet (kontrollerer) to innganger. For eksempel er en differensial som styrer en aksel i en bil et lignende gir.
Slike systemer fungerer etter samme prinsipp som parallelle akselkonstruksjoner. Selv et enkelt planetgir har to innganger, det faste ringgiret er en konstant inngang med null vinkelhastighet.
Detaljert beskrivelse av enheter
Blandede planetariske strukturer kan ha et forskjellig antall hjul, samt forskjellige gir som de er koblet til. Tilstedeværelsen av slike detaljer utvider mekanismens muligheter. Sammensatte planetstrukturer kan settes sammen slik at akselen til bæreplattformen beveger seg med høy hastighet. Som et resultat kan noen problemer med reduksjonsutstyr, solutstyr og andre elimineres i prosessen med å forbedre enheten.
Dermed sett fragitt informasjon, fungerer planetmekanismen etter prinsippet om å overføre rotasjon mellom lenker som er sentrale og mobile. Samtidig er komplekse systemer mer etterspurt enn enkle.
Konfigurasjons alternativer
Det er mulig å bruke hjul (tannhjul) med forskjellige konfigurasjoner i planetmekanismen. Egnet standard med rette tenner, spiralformet, orm, chevron. Type inngrep vil ikke påvirke det generelle prinsippet for drift av planetmekanismen. Hovedsaken er at rotasjonsaksene til bæreren og de sentrale hjulene faller sammen. Men aksene til satellittene kan være plassert i andre plan (kryssende, parallelle, kryssende). Et eksempel på krysset er en mellomhjulsdifferensial, der girene er koniske. Et eksempel på krysset er en selvlåsende differensial med snekkegir (Torsen).
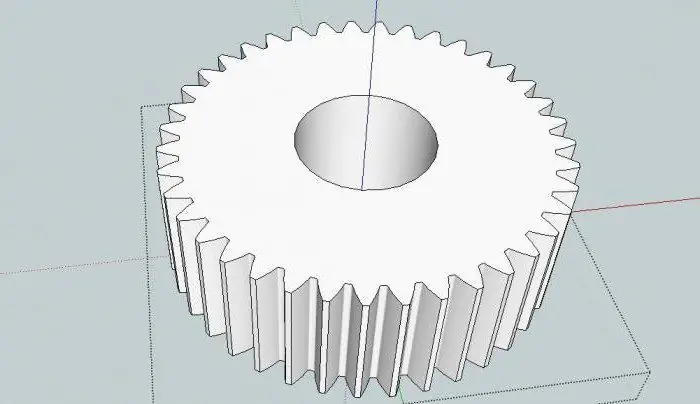
Enkle og komplekse enheter
Som nevnt ovenfor inkluderer planen for planetmekanismen alltid en bærer og to sentrale hjul. Det kan være et hvilket som helst antall satellitter. Dette er den såk alte enkle eller elementære enheten. I slike mekanismer kan design være som følger: "SVS", "SVE", "EVE", hvor:
- S er solen.
- B - transportør.
- E er episenteret.
Hvert slikt sett med hjul + satellitter kalles et planetgirsett. I dette tilfellet må alle hjul rotere i samme plan. Enkle mekanismer er enkelt- og dobbeltrad. De brukes sjelden i ulike tekniske enheter og maskiner. Et eksempelkan tjene som en planetarisk sykkelmekanisme. I henhold til dette prinsippet fungerer hylsen, takket være hvilken bevegelsen utføres. Designet ble laget i henhold til "SVE"-ordningen. Satellitter i ikke 4 deler. I dette tilfellet er solen stivt festet til aksen til bakhjulet, og episenteret er bevegelig. Den blir tvunget til å rotere av en syklist som trykker på pedalene. I dette tilfellet kan overføringshastigheten, og dermed rotasjonshastigheten, endres.
Ofte kan du finne komplekse planetmekanismer. Deres ordninger kan være veldig forskjellige, noe som avhenger av hva dette eller det designet er ment for. Som regel består komplekse mekanismer av flere enkle, laget i henhold til den generelle regelen for et planetgir. Slike komplekse systemer er to-, tre- eller firerader. Teoretisk sett er det mulig å lage strukturer med et stort antall rader, men i praksis skjer ikke dette.
Planare og romlige enheter
Noen tror at et enkelt planetgir må være flatt. Dette er bare delvis sant. Komplekse enheter kan også være flate. Dette betyr at planetgirene, uansett hvor mange av dem som brukes i enheten, er i ett eller parallelle plan. Romlige mekanismer har planetgir i to eller flere plan. I dette tilfellet kan hjulene i seg selv være mindre enn i den første utførelsesformen. Merk at den flate planetmekanismen er den samme som den romlige. Forskjellen er bare i området som er okkupert av enheten, det vil si i kompakthet.
Frihetsgrader
Dette er navnet på samlingenrotasjonskoordinater, som lar deg bestemme posisjonen til systemet i rommet på et gitt tidspunkt. Faktisk har hver planetarisk mekanisme minst to frihetsgrader. Det vil si at vinkelhastighetene for rotasjon av enhver kobling i slike enheter ikke er lineært relatert, som i andre gir. Dette lar deg få utgangsvinkelhastigheter som ikke er de samme som ved inngangen. Dette kan forklares med det faktum at i differensialforbindelsen i planetmekanismen er det tre elementer i en hvilken som helst rad, og resten vil være forbundet med den lineært, gjennom et hvilket som helst element i raden. Teoretisk sett er det mulig å lage planetsystemer med tre eller flere frihetsgrader. Men i praksis er de ubrukelige.

Planetary Gear Ratio
Dette er den viktigste egenskapen til rotasjonsbevegelse. Den lar deg bestemme hvor mange ganger kraftmomentet på den drevne akselen har økt i forhold til momentet til drivakselen. Du kan bestemme girforholdet ved å bruke formlene:
i=d2/d1=Z2/Z1=M2/M1=W1/W2=n1/n2, hvor:
- 1 - ledende link.
- 2 - slavelink.
- d1, d2 - diametrene til det første og andre leddet.
- Z1, Z2 - antall tenner.
- M1, M2 er dreiemomenter.
- W1 W2 - vinkelhastigheter.
- n1 n2 - speed.
Dermed, når girforholdet er høyere enn én på den drevne akselen, øker kraftmomentet, og frekvensen og vinkelhastigheten reduseres. Dette bør alltid tas i betraktning når du lager et design, fordigirforholdet i planetmekanismer avhenger av hvor mange tenner hjulene har, og hvilket element i raden som er det ledende.
Anvendelsesomfang
I dagens verden er det mange forskjellige maskiner. Mange av dem fungerer ved hjelp av planetgir.
De brukes i bildifferensialer, planetgir, i kinematiske skjemaer for komplekse maskinverktøy, i girkasser for flymotorer, i sykler, i skurtreskere og traktorer, i stridsvogner og annet militært utstyr. I henhold til prinsippene for planetgir fungerer mange girkasser i stasjonene til elektriske generatorer. Vurder et annet slikt system.
Planetarisk svingutstyr
Denne designen brukes i noen traktorer, beltekjøretøyer og tanker. Et enkelt diagram av enheten er vist i figuren nedenfor.
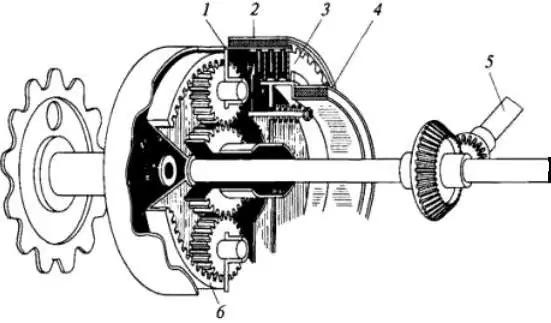
Prinsippet for drift av planetrotasjonsmekanismen er som følger: bæreren (posisjon 1) er koblet til bremsetrommelen (2) og drivhjulet plassert i larven. Episykkelen (6) er koblet til girakselen (posisjon 5). Solen (8) er koblet til clutchskiven (3) og svingbremsetrommelen (4). Når låsekoblingen er koblet inn og båndbremsene er slått av, vil ikke satellittene rotere. De vil bli som spaker, ettersom de er forbundet med solen (8) og episykkelen (6) ved hjelp av tenner. Derfor tvinger de dem og bæreren til å rotere rundt en felles akse samtidig. I dette tilfellet er vinkelhastigheten den samme.
Når du kobler fra låsekoblingen og setter på bremsenå snu solen vil begynne å stoppe, og satellittene vil begynne å bevege seg rundt aksene sine. Dermed skaper de et øyeblikk på bæreren og roterer drivhjulet til larven.
Wear
Når det gjelder levetid og demping, i lineære planetsystemer er lastfordelingen merkbar blant hovedkomponentene.
Termisk og syklisk tretthet kan øke i dem på grunn av den begrensede lastfordelingen og det faktum at planetgir kan rotere ganske raskt på aksene. Dessuten, ved høye hastigheter og utvekslingsforhold til planetgiret, kan sentrifugalkrefter øke mengden bevegelse betraktelig. Det bør også bemerkes at etter hvert som produksjonsnøyaktigheten avtar og antallet satellitter øker, øker tendensen til ubalanse.
Disse enhetene og deres systemer kan til og med være utsatt for slitasje. Noen design vil være følsomme for selv små ubalanser og kan kreve kvalitet og dyre monteringskomponenter. Den nøyaktige plasseringen av planettappene rundt solhjulets akse kan være en nøkkel.
Andre planetariske arrangementer som hjelper til med å balansere laster inkluderer bruk av flytende underenheter eller "myke" fester for å holde solen eller episenteret i bevegelse så lenge som mulig.

Fundamentals of syntese av planetariske enheter
Denne kunnskapen er nødvendig når du designer og lager maskinkomponenter. Konseptet med "syntese av planetariske mekanismer" er å beregne antall tenneri sola, episenter og satellitter. I dette tilfellet må en rekke betingelser være oppfylt:
- Girforholdet må være lik innstilt verdi.
- Inngrep med tannhjul må være riktig.
- Det er nødvendig å sørge for justering av inngående aksel og utgående aksel.
- Nabolag kreves (satelitter må ikke forstyrre hverandre).
I tillegg, når du designer, må du ta hensyn til dimensjonene til den fremtidige strukturen, dens vekt og effektivitet.
Hvis girforholdet (n) er gitt, må antall tenner på solen (S) og på planetgirene (P) tilfredsstille ligningen:
n=S/P
Hvis vi antar at antall tenner ved episenteret er tidlig (A), så med bæreren låst, bør likheten observeres:
n=-S/A
Hvis episenteret er løst, vil følgende likhet være sann:
n=1+ A/S
Dette er hvordan planetmekanismen beregnes.

Fordeler og ulemper
Det finnes flere typer overføringer som er vellykket brukt i ulike enheter. Planetary blant dem skiller seg ut for følgende fordeler:
- Gir mindre belastning på hver tann på hjulene (både solen, og episenteret og satellitter) på grunn av at belastningen på dem er jevnere fordelt. Dette har en positiv effekt på konstruksjonens levetid.
- Med samme kraft har planetgiret mindre dimensjoner og vekt enn andre typer girkasser.
- Mulighet til å oppnå høyere girforhold medfærre hjul.
- Sørg for mindre støy.
Ulemper med planetgir:
- Trenger mer presisjon i produksjonen deres.
- Lav effektivitet med et relativt stort utvekslingsforhold.






