Når de studerer i fysikk den mekaniske bevegelsen til kropper i rommet, tar de alltid hensyn til den resulterende akselerasjonen. La oss vurdere i artikkelen hva akselerasjon er, og hvordan det betegnes i fysikk, og også løse et enkelt problem for å beregne denne verdien.
Hva er akselerasjon og hva er dens typer?
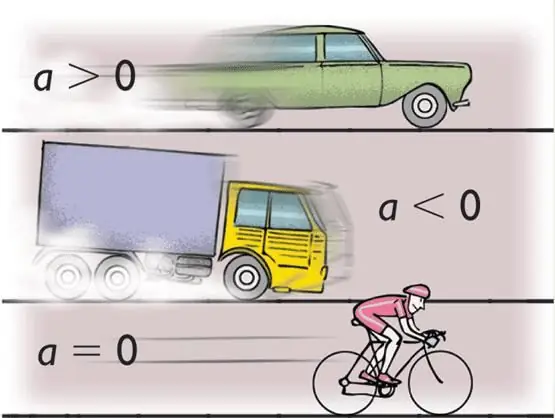
Under akselerasjonen forstå verdien, hvis betydning er hastigheten på endring i kroppens hastighet. Matematisk er denne definisjonen skrevet som følger:
a=dv/dt.
Hvis tidsfunksjonen til hastighet er kjent, er det nok å finne dens førstederiverte for å beregne akselerasjonen på et gitt tidspunkt.
I fysikk er akselerasjonsbokstaven liten latin a. Dette er imidlertid den såk alte lineære akselerasjonen, som måles i enheter av m/s2. I tillegg til det er det også vinkelakselerasjon. Den viser endringen i vinkelhastighet og uttrykkes i enheter av rad/s2. Denne typen akselerasjon er betegnet med den greske små bokstaven α (alfa). Noen gangerbokstaven ε (epsilon) brukes for å betegne det.
Hvis kroppen beveger seg langs en buet bane, blir den totale akselerasjonen dekomponert i to komponenter: tangentiell (bestemmer endringen i hastighet i størrelse) og normal (bestemmer endringen i hastighet i retning). Disse akselerasjonstypene er også betegnet med bokstavene a, men ved å bruke de tilsvarende indeksene: at og a. Normal kalles ofte sentripetal, og tangentiell kalles ofte tangent.
Til slutt er det en annen type akselerasjon som oppstår når kropper faller fritt i planetens gravitasjonsfelt. Det er merket med bokstaven g.
Problem i fysikk for akselerasjon
Det er kjent at kroppen beveger seg i en rett linje. Hastigheten over tid bestemmes av følgende lov:
v=2t2-t+4.
Det er nødvendig å beregne akselerasjonen som kroppen vil ha til tiden t=2,5 sekunder.
Etter definisjonen av a får vi:
a=dv/dt=4t - 1.
Det vil si at verdien a avhenger lineært av tid. Det er merkelig å merke seg at i det første øyeblikket (t=0) var akselerasjonen negativ, det vil si rettet mot hastighetsvektoren. Vi får svaret på problemet ved å sette inn t=2,5 sekunder i denne ligningen: a=9 m/s2.






