Proposisjonalgebra er en eksakt vitenskap som ikke går på akkord. For å løse eksempler med konjunksjon, disjunksjon, implikasjon og så videre, kan du bygge en sannhetstabell i Excel-applikasjonen. Den er utstyrt med et sett med logiske funksjoner som automatiserer og forenkler prosessen med å finne resultatet.
Matematisk logikk: grunnleggende konsepter
Aristoteles regnes som grunnleggeren av formell logikk. På 1600-tallet G. Leibniz foreslo å introdusere symboler for å definere utsagn. D. Buhl konsoliderte den ervervede kunnskapen og markerte for første gang setninger med symboler.
Skjematisk er "TRUE" erstattet med 1, og "FALSE" med 0.
Under uttalelsen forstås enhver deklarativ setning som gir informasjon og er i stand til å ta verdien av sannhet eller usannhet. I algebra abstraheres logikk fra den semantiske belastningen av setninger og vurderer kun logiske verdier.
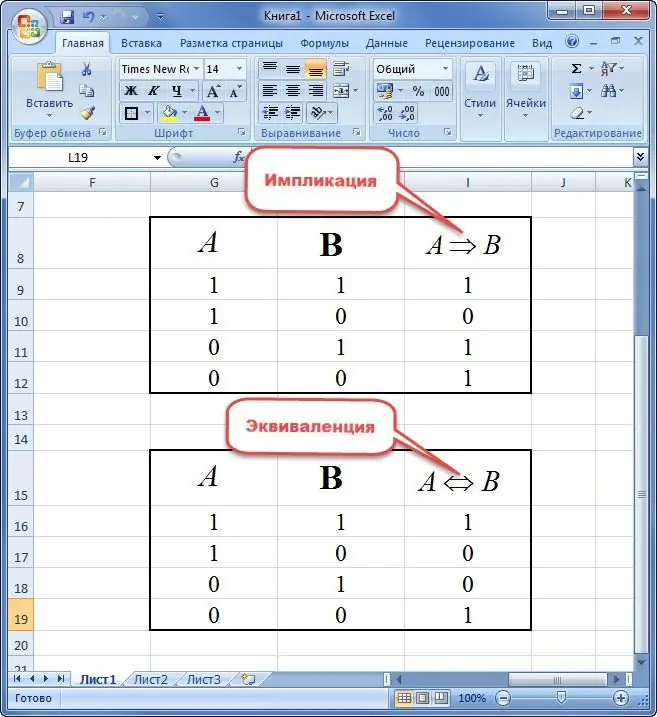
Negasjon er et nytt uttrykk som tar verdien av sant hvis det er usant og omvendt.
Konjunksjon av tovariabler kalles en ny setning, som tar verdien av sannhet i tilfelle av samtidig betegnelse "1" og usannhet i andre situasjoner.
Disjunksjonen av to utsagn forstås som et nytt uttrykk som tar verdien "FALSE" bare hvis det er "0" og "TRUE" i andre varianter samtidig.
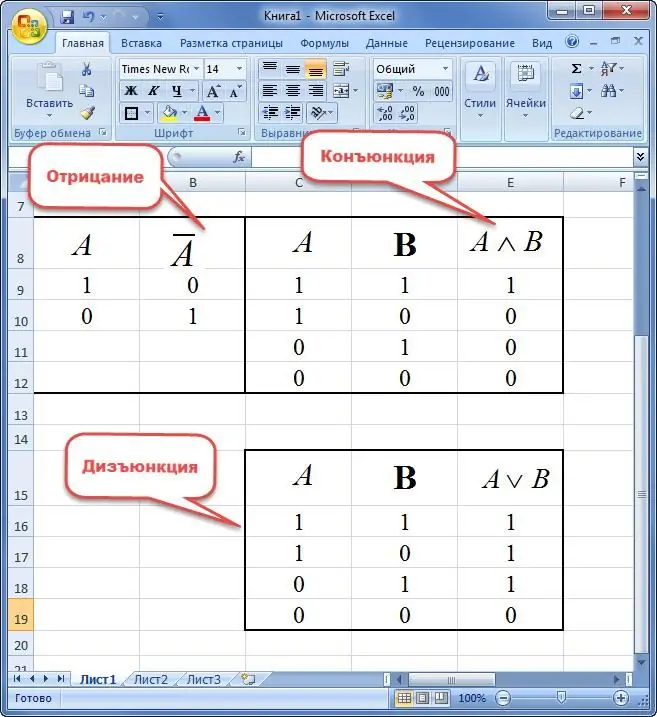
En implikasjon av to variabler er en ny setning der:
- hvis premisset er sant og konsekvensen er usann, er uttrykket lik "0";
- utsagn er lik "1" i andre tilfeller.
Ekvivalent av to variabler er forstått som et nytt utsagn som tar verdien av sannhet bare hvis elementene er like. Ellers er tilbudet "0".
Logiske verdier for uttrykk presenteres vanligvis i tabellform. Det er et annet navn for denne typen informasjon. De sier at for en uttalelse må du bygge en sannhetstabell. Den spesifiserer startverdiene for alle variabler, og deretter beregnes resultatet av hele uttrykket.
Algorithme for implementering av beregninger i logiske operasjoner
For å bygge en sannhetstabell må du vite rekkefølgen handlingene utføres i. I et uttrykk med flere operander utføres beregningen i følgende rekkefølge:
- inversjon (negasjon);
- konjunksjon (logisk funksjon i Excel "AND");
- disjunction (boolsk operator i Excel "ELLER");
- implikasjon (konsekvens);
- ekvivalens.
Det er to operasjoner til, men deres prioritet er ikke definert:
- Schaeffers slag;
- Pierce-pil.
Beregningsalgoritmen endres hvis uttrykket er omsluttet av parentes.
Rekkefølgen for å konstruere en tabellform for logiske operander i Excel
Før du finner verdien av et uttrykk, må du studere konseptet med en logisk algebraformel. Definisjonen sier at dette er et komplekst uttrykk, bestående av de enkleste utsagnene forbundet med logiske operander.
Eksempel 1. Konstruer en sannhetstabell for konjunksjon, disjunksjon og negasjon.
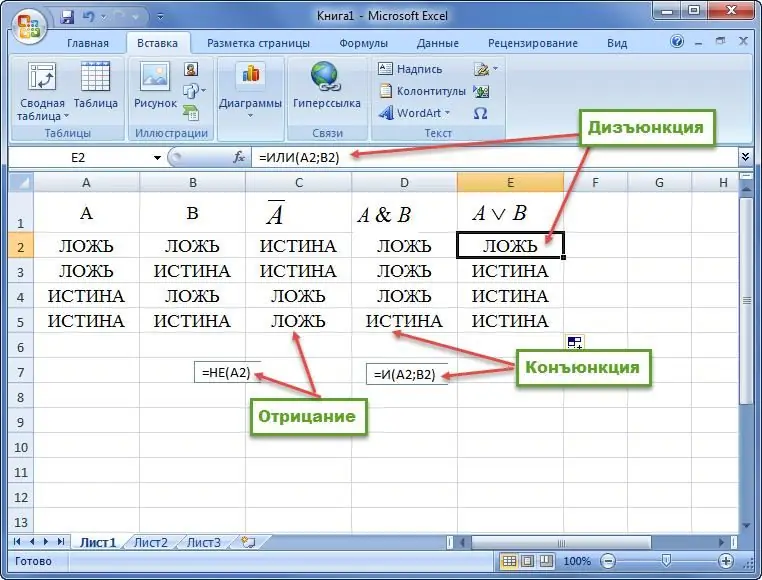
Eksempel 2. Gitt en formel for logikkens algebra. Bygg en sannhetstabell. Eksempler er gitt nedenfor.
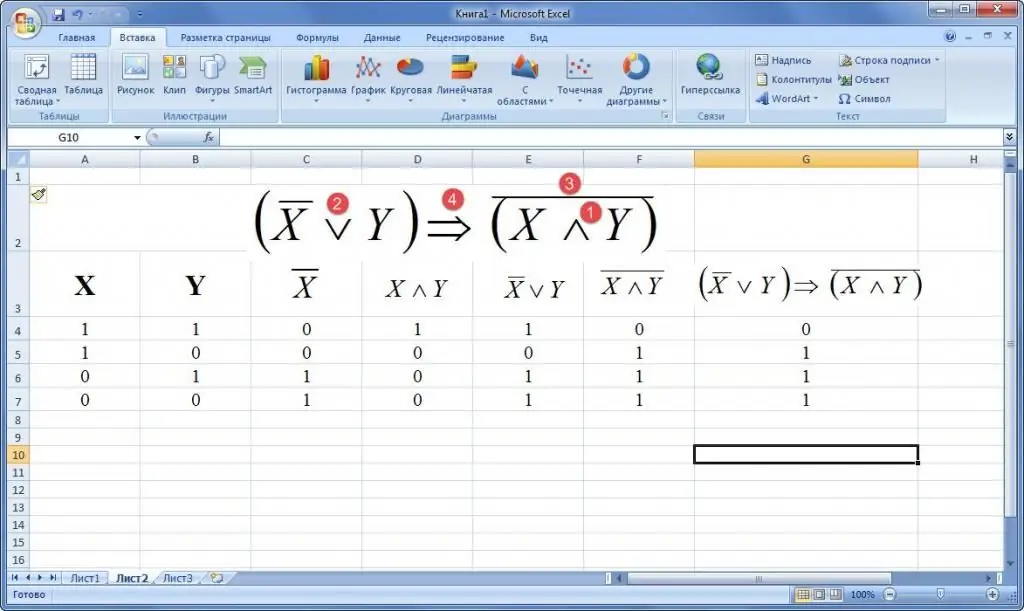
Eksempel 3. Hvordan bygge en sannhetstabell i Excel, gitt en formel for logisk algebra i en verbal beskrivelse. Å si: "Hvis en trekant er likesidet, så er alle kantene like eller alle vinklene like."
Først må du analysere den sammensatte setningen til minimale elementer:
- Den første delen av uttrykket: A="likesidet trekant".
- Second: B="alle sider av figuren er like".
- Tredje: C="alle vinkler i en trekant er like".
Deretter blir et uttrykk kompilert og løst i Excel-programvarepakken.
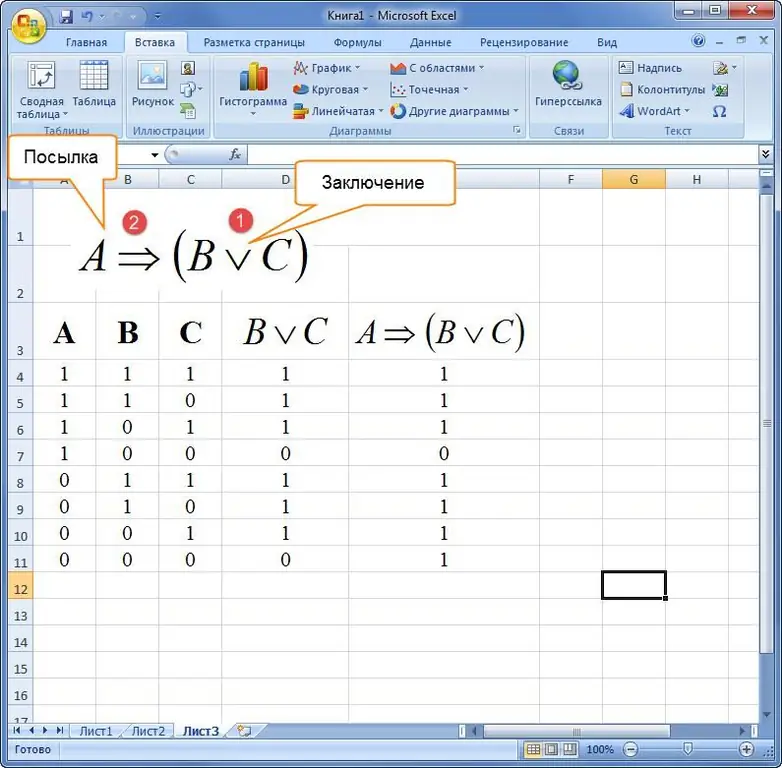
Når du kompilerer sannhetstabeller, er det viktig å huske rekkefølgen på operasjonene.






