Temaet for dagens artikkel vil være kinematikken til et materiell punkt. Hva handler det om? Hvilke konsepter vises i den og hvilken definisjon bør gis til dette begrepet? Vi vil prøve å svare på disse og mange andre spørsmål i dag.
Definisjon og konsept
Kinematikk til et materiell punkt er ikke noe mer enn en underseksjon av fysikk k alt "mekanikk". Hun studerer på sin side bevegelsesmønstrene til visse kropper. Kinematikken til et materiell punkt behandler også dette problemet, men gjør det ikke på en generell måte. Faktisk studerer denne underseksjonen metoder som lar deg beskrive bevegelsen av kropper. I dette tilfellet er det kun de såk alte idealiserte kroppene som egner seg for forskning. Disse inkluderer: en materiell spiss, en absolutt stiv kropp og en ideell gass. La oss vurdere konseptene mer detaljert. Vi vet alle fra skolebenken at det er vanlig å kalle et materiell punkt en kropp, hvis dimensjoner i en gitt situasjon kan neglisjeres. Forresten begynner kinematikken til translasjonsbevegelsen til et materiell punkt for første gangvises i fysikklærebøker i sjuende klasse. Dette er den enkleste grenen, så det er mest praktisk å begynne å bli kjent med vitenskapen med dens hjelp. Et eget spørsmål er hva som er elementene i kinematikken til et materiell punkt. Det er ganske mange av dem, og betinget kan de deles inn i flere nivåer med ulik kompleksitet for forståelse. Hvis vi for eksempel snakker om radiusvektoren, er det i prinsippet ikke noe uoverkommelig komplisert i definisjonen. Du vil imidlertid være enig i at det vil være mye lettere for en elev å forstå det enn for en elev på ungdomsskolen eller videregående. Og for å være ærlig, er det ikke nødvendig å forklare funksjonene i denne terminen for elever på videregående skole.
En kort historie om etableringen av kinematikk
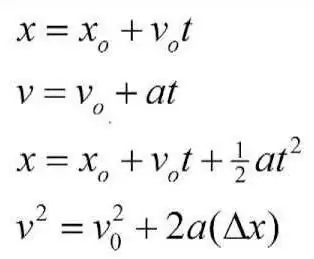
For mange, mange år siden viet den store vitenskapsmannen Aristoteles brorparten av fritiden sin til studiet og beskrivelsen av fysikk som en egen vitenskap. Han jobbet også med kinematikk, og prøvde å presentere hovedtesene og konseptene, på en eller annen måte brukt i forsøk på å løse praktiske og til og med hverdagslige problemer. Aristoteles ga de første ideene om hva elementene i kinematikken til et materiell punkt er. Hans verk og verk er svært verdifulle for hele menneskeheten. Likevel gjorde han i sine konklusjoner et betydelig antall feil, og årsaken til dette var visse misoppfatninger og feilberegninger. På et tidspunkt ble en annen vitenskapsmann, Galileo Galilei, interessert i verkene til Aristoteles. En av de grunnleggende tesene fremsatt av Aristoteles var at bevegelsen til en kroppoppstår bare hvis den påvirkes av en eller annen kraft, bestemt av intensitet og retning. Galileo beviste at dette var en feil. Kraften vil påvirke parameteren for bevegelseshastighet, men ikke mer. Italieneren viste at kraft er årsaken til akselerasjon, og den kan bare oppstå gjensidig med den. Galileo Galilei ga også betydelig oppmerksomhet til studiet av prosessen med fritt fall, og utledet de passende mønstrene. Sannsynligvis husker alle hans berømte eksperimenter, som han utførte på det skjeve tårnet i Pisa. Fysikeren Ampère brukte også det grunnleggende om kinematiske løsninger i sine arbeider.
Innledende konsepter
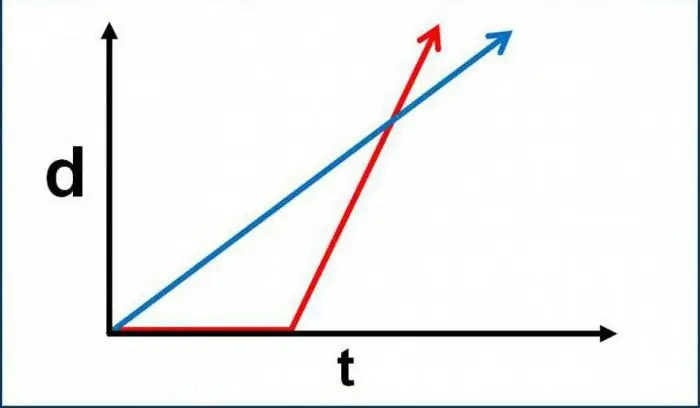
Som nevnt tidligere, er kinematikk studiet av måter å beskrive bevegelsen til idealiserte objekter. I dette tilfellet kan det grunnleggende om matematisk analyse, vanlig algebra og geometri brukes i praksis. Men hvilke begreper (nøyaktig begreper, og ikke definisjoner for parametriske størrelser) ligger til grunn for denne underdelen av fysikk? For det første bør alle tydelig forstå at kinematikken til translasjonsbevegelsen til et materiell punkt tar hensyn til bevegelse uten å ta hensyn til kraftindikatorer. Det vil si at for å løse de tilsvarende problemene trenger vi ikke formler knyttet til kraft. Det tas ikke i betraktning av kinematikk, uansett hvor mange av dem det er - en, to, tre, minst flere hundre tusen. Likevel er eksistensen av akselerasjon fortsatt gitt. I en rekke problemer foreskriver kinematikken til bevegelsen til et materialpunkt å bestemme størrelsen på akselerasjonen. Imidlertid er årsakene til dette fenomenet (det vil si kreftene ogderes natur) blir ikke vurdert, men utelatt.
klassifisering
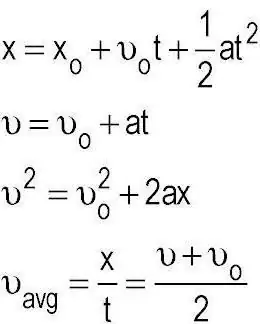
Vi fant ut at kinematikk utforsker og bruker metoder for å beskrive bevegelser av kropper uten hensyn til kreftene som virker på dem. Forresten, en annen underseksjon av mekanikk, som kalles dynamikk, omhandler en slik oppgave. Allerede der brukes Newtons lover, som i praksis gjør det mulig å bestemme ganske mange parametere med en liten mengde kjente initialdata. De grunnleggende begrepene for kinematikken til et materiell punkt er rom og tid. Og i forbindelse med utviklingen av vitenskapen både generelt og på dette området, oppsto spørsmålet om hensiktsmessigheten av å bruke en slik kombinasjon.
Helt fra begynnelsen var det klassisk kinematikk. Vi kan si at det ikke bare er preget av tilstedeværelsen av både tidsmessige og romlige hull, men også deres uavhengighet fra valget av en eller annen referanseramme. Vi skal forresten snakke om dette litt senere. La oss nå bare forklare hva vi snakker om. I dette tilfellet vil et segment betraktes som et romlig intervall, og et tidsintervall vil betraktes som et tidsintervall. Alt ser ut til å være klart. Så disse hullene vil bli betraktet i klassisk kinematikk som absolutte, invariante, med andre ord uavhengig av overgangen fra en referanseramme til en annen. Hvorvidt virksomheten relativistisk kinematikk. I den kan gapene under overgangen mellom referansesystemer endres. Det ville enda mer riktig å si at de ikke kan, men det må de sannsynligvis. På grunn av dette, samtidigheten av de totilfeldige hendelser blir også relative og gjenstand for spesiell vurdering. Det er derfor i relativistisk kinematikk to begreper - rom og tid - kombineres til ett.
Kinematikk av et materialpunkt: hastighet, akselerasjon og andre mengder
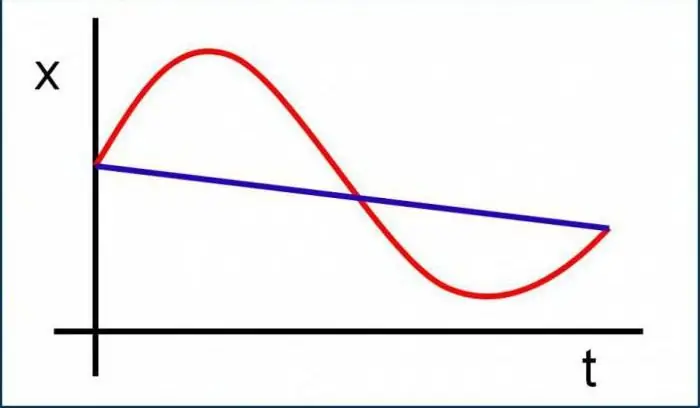
For å forstå i det minste litt denne underdelen av fysikk, må du navigere i de viktigste konseptene, kjenne til definisjonene og forestille deg hva denne eller den mengden er i generelle termer. Det er ikke noe vanskelig i dette, faktisk er alt veldig enkelt og enkelt. Tenk kanskje til å begynne med de grunnleggende konseptene som brukes i kinematikkproblemer.
Movement
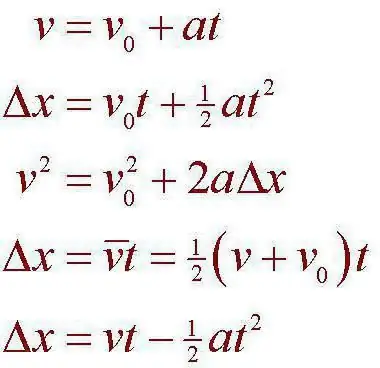
Mekanisk bevegelse vi vil vurdere prosessen der et eller annet idealisert objekt endrer sin posisjon i rommet. I dette tilfellet kan vi si at endringen skjer i forhold til andre kropper. Det er også nødvendig å ta hensyn til det faktum at etableringen av et visst tidsintervall mellom to hendelser skjer samtidig. For eksempel vil det være mulig å isolere et visst intervall dannet i løpet av tiden som har gått mellom kroppen kommer fra en posisjon til en annen. Vi legger også merke til at kroppene i dette tilfellet kan og vil samhandle med hverandre, i henhold til mekanikkens generelle lover. Det er nettopp dette kinematikken til et materialpunkt oftest opererer med. Referansesystemet er det neste konseptet som er uløselig knyttet til det.
Koordinater
De kan kalles vanlige data som lar deg bestemme kroppens posisjon på et eller annet tidspunkt. Koordinater er uløselig knyttet til konseptet med et referansesystem, så vel som koordinatnettet. Oftest er de en kombinasjon av bokstaver og tall.
Radius-vektor
Fra navnet skal det allerede være klart hva det er. Ikke desto mindre, la oss snakke om dette mer detaljert. Hvis et punkt beveger seg langs en bestemt bane, og vi kjenner nøyaktig begynnelsen av et bestemt referansesystem, kan vi tegne en radiusvektor når som helst. Den vil koble startposisjonen til punktet til den øyeblikkelige eller endelige posisjonen.
Trajectory
Det vil bli k alt en kontinuerlig linje, som legges som et resultat av bevegelsen av et materialpunkt i et bestemt referansesystem.
Hastighet (både lineær og vinkel)
Dette er en verdi som kan fortelle hvor fort kroppen går gjennom et bestemt distanseintervall.
akselerasjon (både vinkel og lineær)
Viser etter hvilken lov og hvor intensivt hastighetsparameteren til kroppen endres.
Kanskje, her er de - hovedelementene i kinematikken til et materiell punkt. Det skal bemerkes at både hastighet og akselerasjon er vektorstørrelser. Og dette betyr at de ikke bare har en viss veiledende verdi, men også en viss retning. Forresten, de kan rettes både i én retning og i motsatte retninger. I det første tilfellet vil kroppen akselerere, i det andre vil den bremse.
Enkle oppgaver
Kinematikk til et materiell punkt (hastighet, akselerasjon og avstand som er praktisk t alt grunnleggende konsepter) inkluderer ikke bare et stort antall oppgaver, men mange av deres forskjellige kategorier. La oss prøve å løse et ganske enkelt problem ved å bestemme avstanden kroppen har tilbakelagt.
Anta at forholdene vi har for hånden er som følger. Førerens bil står på startstreken. Operatøren gir klarsignal med flagget, og bilen tar brått av. Bestem om hun kan sette en ny rekord i konkurransen av syklister, hvis den neste lederen dekket en avstand på hundre meter på 7,8 sekunder. Ta bilens akselerasjon lik 3 meter delt på et sekund i kvadrat.
Så, hvordan løser jeg dette problemet? Det er ganske interessant, siden vi er pålagt å ikke "tørke" bestemme visse parametere. Det lysner opp med omsetninger og en viss situasjon, som diversifiserer prosessen med å løse og søke etter indikatorer. Men hva bør vi veiledes av før vi nærmer oss oppgaven?
1. Kinematikken til et materialpunkt sørger for bruk av akselerasjon i dette tilfellet.
2. Løsningen antas å bruke avstandsformelen, siden dens numeriske verdi vises i betingelsene.
Problemet er faktisk løst ganske enkelt. For å gjøre dette tar vi avstandsformelen: S=VoT + (-) AT ^ 2/2. Hva er poenget? Vi må finne ut hvor lenge rytteren vil dekke den angitte distansen, og deretter sammenligne tallet med rekorden for å finne ut om han slår den eller ikke. For å gjøre dette, alloker tid, vi får formelenfor ham: AT^2 + 2VoT - 2S. Dette er ikke noe mer enn en andregradsligning. Men bilen tar av, noe som betyr at starthastigheten vil være 0. Når du løser ligningen, vil diskriminanten være lik 2400. For å finne tiden må du ta roten. La oss gjøre det til andre desimal: 48,98 Finn roten til ligningen: 48,98/6=8,16 sekunder. Det viser seg at sjåføren ikke vil være i stand til å slå den eksisterende rekorden.




