Fra skolen kjenner vi alle regelen om å heve til en potens: ethvert tall med en eksponent N er lik resultatet av å multiplisere dette tallet med seg selv N ganger. Med andre ord, 7 i potensen 3 er 7 multiplisert med seg selv tre ganger, det vil si 343. En annen regel er at å heve en hvilken som helst verdi til 0 gir en, og å heve en negativ verdi er resultatet av vanlig eksponentiering, hvis det er partall, og samme resultat med et minustegn hvis det er oddetall.

Reglene gir også svar på hvordan man kan heve et tall til en negativ potens. For å gjøre dette må du øke den nødvendige verdien med modulen til indikatoren på vanlig måte, og deretter dele enheten med resultatet.
Fra disse reglene blir det klart at gjennomføring av reelle oppgaver med store mengder vil kreve tilgjengelighet av tekniske midler. Manuelt vil det være mulig å multiplisere med seg selv en maksimal rekkevidde av tall opp til tjue eller tretti, og deretter ikke mer enn tre eller fire ganger. Dette er ikke å nevne det faktum at da også dele enheten med resultatet. Derfor, for de som ikke har en spesiell ingeniør for håndenkalkulator, vil vi vise deg hvordan du øker et tall til en negativ potens i Excel.
Løse problemer i Excel
For å løse problemer med eksponentiering lar Excel deg bruke ett av to alternativer.
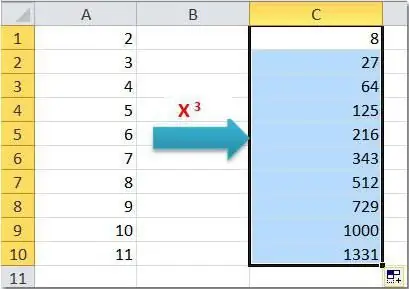
Den første er bruken av formelen med standard hettesymbol. Skriv inn følgende data i regnearkcellene:
| B | C | Formel | Resultat | |
| 2 | 7 | 3 | =B2^C2 | 343 |
På samme måte kan du øke ønsket verdi til en hvilken som helst potens - negativ, brøk. La oss gjøre følgende og svare på spørsmålet om hvordan du hever et tall til en negativ potens. Eksempel:
| B | C | Formel | Resultat | |
| 2 | 7 | -3 | =B2^C2 | 0, 002915 |
Du kan rette=B2^-C2 direkte i formelen.
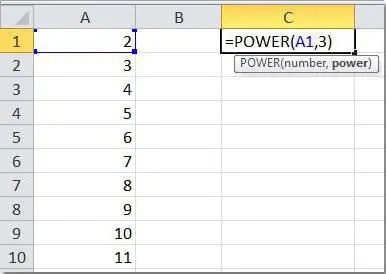
Det andre alternativet er å bruke den ferdige funksjonen "Grad", som tar to obligatoriske argumenter - et tall og en indikator. For å begynne å bruke det, er det nok å sette et "lik" tegn (=) i hvilken som helst ledig celle,peker på begynnelsen av formelen, og skriv inn ordene ovenfor. Det gjenstår å velge to celler som vil delta i operasjonen (eller spesifisere spesifikke tall manuelt), og trykk på Enter-tasten. La oss se på noen enkle eksempler.
| B | C | Formel | Resultat | ||
| 2 | 7 | 3 | =POWER(B2;C2) | 343 | |
| 3 | 7 | -3 | =POWER(B3;C3) |
|
Som du kan se, er det ikke noe komplisert med hvordan man hever et tall til en negativ potens og til en normal potens ved bruk av Excel. Tross alt, for å løse dette problemet, kan du bruke både det velkjente "lokk"-symbolet og den lett å huske innebygde funksjonen til programmet. Dette er et klart pluss!
La oss gå videre til mer komplekse eksempler. La oss huske regelen om hvordan man hever et tall til en negativ potens av brøktegn, og vi vil se at denne oppgaven er veldig enkel å løse i Excel.
Brøkindikatorer
Kort sagt, algoritmen for å beregne et tall med en brøkeksponent er som følger.
- Konverter en brøk til en riktig eller uekte brøk.
- Øv tallet vårt til telleren for den resulterende konverterte brøken.
- Fra tallet oppnådd i forrige avsnitt, beregn roten, med betingelsen at eksponenten til rotenvil være nevneren for brøken oppnådd i det første trinnet.
Enig i at selv når man arbeider med små tall og egenbrøk, kan slike beregninger ta mye tid. Det er bra at regnearkbehandleren Excel ikke bryr seg om hvilket tall og i hvilken grad den skal øke. Prøv å løse følgende eksempel på et Excel-regneark:
| B (tall) | C | Konverter til brøk | Formel | Resultat | |
| 2 | 7 | 0, 4 | 2/5 | =POWER(B2;C2) | 2, 177906424 |
Ved å bruke reglene ovenfor kan du sjekke og forsikre deg om at beregningen er riktig.
På slutten av artikkelen vår, i form av en tabell med formler og resultater, vil vi gi flere eksempler på hvordan man hever et tall til negativ potens, samt flere eksempler med brøktall og potenser.
Eksempeltabell
Sjekk følgende eksempler på Excel-regnearket. For at alt skal fungere riktig, må du bruke en blandet referanse når du kopierer formelen. Fest nummeret på kolonnen som inneholder tallet som heves, og nummeret på raden som inneholder indikatoren. Formelen din skal se omtrent slik ut: "=$B4^C$3".
| Number/Degree | 1 | 2 | 3 | 0, 5 | -0, 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 1, 414214 | 0, 707107 |
| 7 | 7 | 49 | 343 | 2, 645751 | 0, 377964 |
| -7 | -7 | 49 | -343 | NUMBER! | NUMBER! |
| 0, 2 | 0, 2 | 0, 04 | 0, 008 | 0, 447214 | 2, 236068 |
| 0, 4 | 0, 4 | 0, 16 | 0, 064 | 0, 632456 |
1, 581139 |
| -0, 4 | -0, 4 | 0, 16 | -0, 064 | NUMBER! | NUMBER! |
Vær oppmerksom på at positive tall (selv ikke-heltalls) beregnes uten problemer for noen eksponenter. Det er ingen problemer med å heve noen tall til heltall. Men å heve et negativt tall til en brøkpotens vil bli en feil for deg, siden det er umulig å følge regelen som er angitti begynnelsen av artikkelen vår om konstruksjonen av negative tall, fordi paritet er en karakteristikk av et utelukkende HELLERTall.






