Gasser, fra termodynamikkens synspunkt, er beskrevet av et sett med makroskopiske egenskaper, hvorav de viktigste er temperatur, trykk og volum. Konstansen til en av disse parameterne og endringen i de to andre indikerer at en eller annen isoprosess forekommer i gassen. Vi vil vie denne artikkelen til et detaljert svar på spørsmålene om at dette er en isokorisk prosess, hvordan den skiller seg fra isotermiske og isobariske endringer i tilstandene til et gasssystem.
Ideell gass i fysikk

Før du svarer på spørsmålet om at dette er en isokorisk prosess, bør du bli bedre kjent med konseptet om en ideell gass. I fysikk forstås det som enhver gass der den gjennomsnittlige kinetiske energien til dens bestanddeler langt overstiger den potensielle energien til deres interaksjon, og avstandene mellom disse partiklene er flere størrelsesordener større enn deres lineære dimensjoner. Under de angitte forholdene er det mulig når du utførerberegninger tar ikke hensyn til interaksjonsenergien mellom partikler (den er lik null), og det kan også antas at partiklene er materialpunkter med en viss masse m.
Den eneste prosessen som finner sted i en ideell gass er kollisjonen av partikler med veggene i karet som inneholder stoffet. Disse kollisjonene viser seg i praksis som eksistensen av et visst trykk i gassen P.
Som regel kan ethvert gassformet stoff som består av relativt kjemisk inerte molekyler og som har lavt trykk og høye temperaturer betraktes som en ideell gass med tilstrekkelig nøyaktighet for praktiske beregninger.
Ligning som beskriver en ideell gass
Selvfølgelig snakker vi om den universelle loven til Clapeyron-Mendeleev, som bør forstås godt for å forstå at dette er en isokorisk prosess. Så den universelle tilstandsligningen har følgende form:
PV=nRT.
Det vil si at produktet av trykket P og gassvolumet V er lik produktet av den absolutte temperaturen T og stoffmengden i mol n, der R er proporsjonalitetsfaktoren. Selve ligningen ble først skrevet ned av Emile Clapeyron i 1834, og på 70-tallet av 1800-tallet erstattet D. Mendeleev et sett med konstante verdier av en enkelt universell gasskonstant R (8,314 J/(molK))).
I samsvar med Clapeyron-Mendeleev-ligningen, i et lukket system forblir antallet gasspartikler konstant, så det er bare tre makroskopiske parametere som kan endres (T, Pog V). Det siste faktum ligger til grunn for forståelsen av de ulike isoprosessene som vil bli diskutert nedenfor.
Hva er en isokorisk prosess?
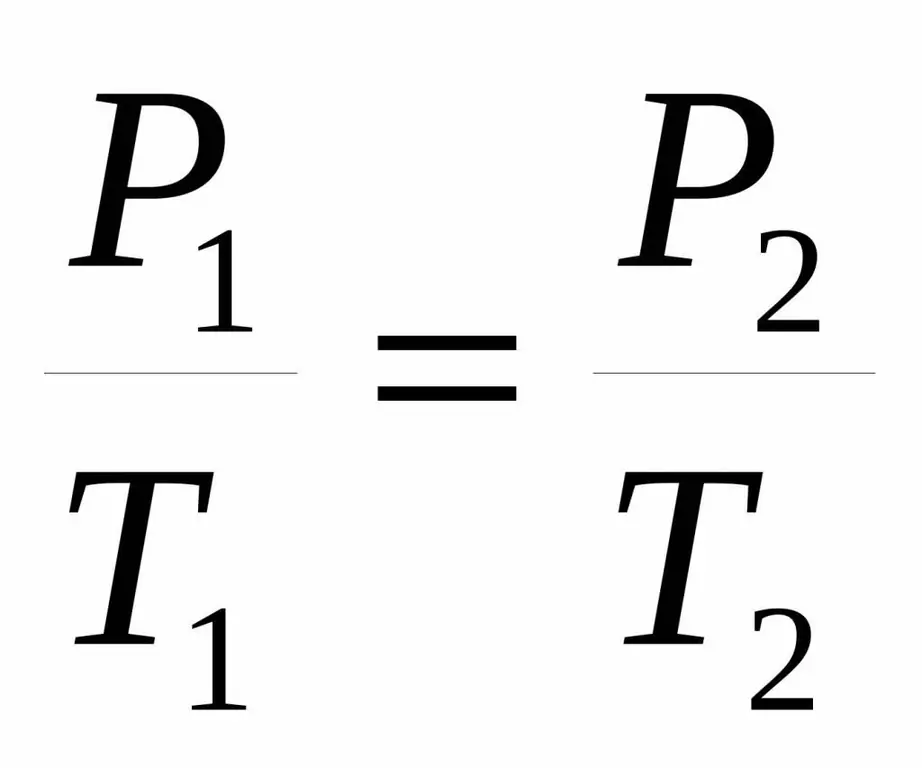
Denne prosessen forstås som absolutt enhver endring i systemets tilstand, der volumet er bevart.
Hvis vi vender oss til den universelle tilstandsligningen, kan vi si at i en isokorisk prosess endres bare trykk og absolutt temperatur i en gass. For å forstå nøyaktig hvordan de termodynamiske parameterne endres, skriver vi det tilsvarende matematiske uttrykket:
P / T=konst.
Noen ganger gis denne likheten i en litt annen form:
P1 / T1=P2 / T 2.
Begge likheter kalles Charles' lov etter navnet på en fransk vitenskapsmann som på slutten av 1700-tallet oppnådde den bemerkede avhengigheten eksperimentelt.

Hvis vi bygger en graf av funksjonen P(T), så får vi en rettlinjet avhengighet, som kalles en isokor. Enhver isokor (for alle verdier av n og V) er en rett linje.
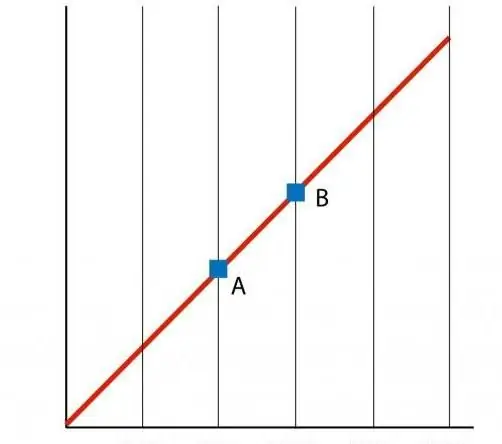
Energibeskrivelse av prosessen
Som nevnt er en isokorisk prosess en endring i tilstanden til et system som finner sted i et lukket, men ikke isolert system. Vi snakker om muligheten for varmeveksling mellom gassen og miljøet. Generelt fører enhver tilførsel av varme Q til systemet til to resultater:
- endrer intern energi U;
- gassfungerer A, utvider eller trekker seg sammen.
Den siste slutningen skrives matematisk som følger:
Q=U + A.
Den isokoriske prosessen til en ideell gass, etter sin definisjon, innebærer ikke arbeid utført av gassen, siden volumet forblir uendret. Dette betyr at all varmen som tilføres systemet går til å øke dets interne energi:
Q=U.
Hvis vi erstatter den eksplisitte formelen for intern energi i dette uttrykket, kan varmen fra den isokoriske prosessen representeres som:
Q=z / 2nRT.
Her er z antallet frihetsgrader, som bestemmes av den polyatomiske naturen til molekylene som utgjør gassen. For en monoatomisk gass er z=3, for en diatomisk gass - 5, og for en triatomisk gass - 6. Her, under frihetsgradene, mener vi translasjons- og rotasjonsgrader.
Hvis vi sammenligner effektiviteten ved oppvarming av et gasssystem i isokoriske og isobariske prosesser, vil vi i det første tilfellet få maksimal effektivitet, siden under den isobariske endringen i systemets tilstand, ekspanderer gassen, og en del av varmetilførselen går til arbeid.
Isobarisk prosess
Ovenfor har vi beskrevet i detalj at dette er en isokorisk prosess. La oss nå si noen ord om andre isoprosesser. La oss starte med isobarisk. Basert på navnet forstås det som overgangen til systemet mellom tilstander ved konstant trykk. Denne prosessen er beskrevet av Gay-Lussac-loven som følger:
V / T=const.
Som med isokoren, representerer V(T)-isobaren også en rett linje på grafen.
Forav enhver isobarisk prosess, er det praktisk å beregne arbeidet utført av gassen, siden det er lik produktet av konstant trykk og volumendringen.
Isotermisk prosess
Dette er en prosess der temperaturen i systemet forblir konstant. Det er beskrevet av Boyle-Mariotte-loven for en ideell gass. Det er merkelig å merke seg at dette er den første eksperimentelt oppdagede gassloven (andre halvdel av 1600-tallet). Den matematiske notasjonen ser slik ut:
PV=const.
Isokoriske og isotermiske prosesser er forskjellige når det gjelder deres grafiske representasjon, siden funksjonen P(V) er en hyperbolsk, ikke en lineær sammenheng.
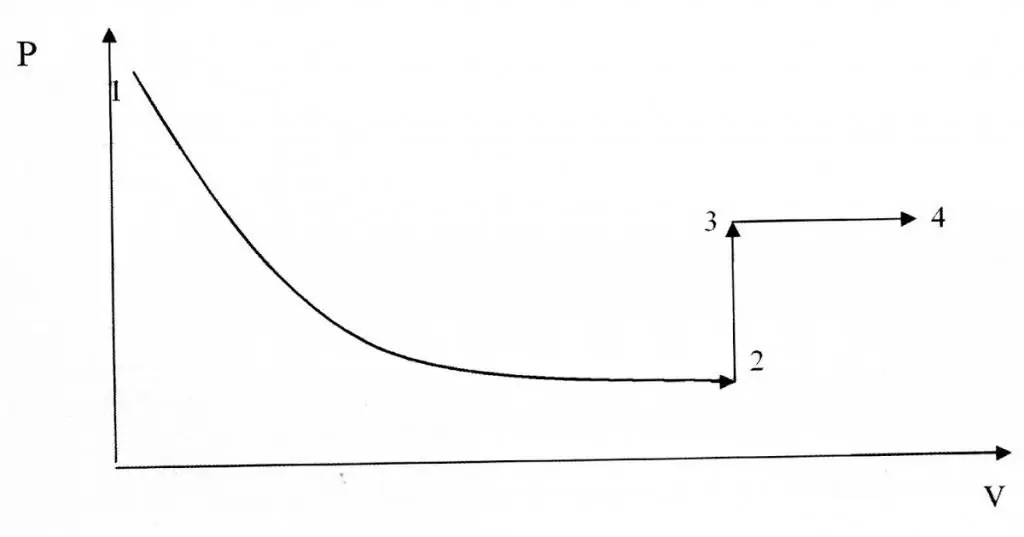
Eksempel på problemløsning
La oss konsolidere den teoretiske informasjonen gitt i artikkelen ved hjelp av deres søknad for å løse et praktisk problem. Det er kjent at rent gassformig nitrogen var i en sylinder ved et trykk på 1 atmosfære og en temperatur på 25 °C. Etter at gassflasken var varmet opp og trykket i den ble målt, viste det seg å være 1,5 atmosfærer. Hva er temperaturen på gassen i sylinderen etter oppvarming? Hvor mye endret den indre energien til gassen seg hvis det var 4 mol nitrogen i ballongen.
For å svare på det første spørsmålet bruker vi følgende uttrykk:
P1 / T1=P2 / T 2.
Hvorfra vi kommer:
T2=P2 / P1 T 1.
I dette uttrykket kan trykk erstattes i vilkårlige enhetermålinger, siden de krymper, og temperaturen kun er i kelvin. Når det er sagt, får vi:
T2=1,5 /1298,15=447,224 K.
Den beregnede temperaturen i grader Celsius er 174 °C.
Siden nitrogenmolekylet er diatomisk, kan endringen i dets indre energi under oppvarming bestemmes som følger:
ΔU=5 / 2nRΔT.
Ved å erstatte de kjente verdiene i dette uttrykket vil vi få svaret på det andre spørsmålet i oppgaven: ΔU=+12,4 kJ.






