Isokorisk varmekapasitet til en ideell gass

2024 Forfatter: Angel Austin | [email protected]. Sist endret: 2023-12-17 05:37

I termodynamikk, når man studerer overganger fra den initiale til den endelige tilstanden til et system, er det viktig å kjenne til den termiske effekten av prosessen. Begrepet varmekapasitet er nært knyttet til denne effekten. I denne artikkelen vil vi ta for oss spørsmålet om hva som menes med den isokoriske varmekapasiteten til en gass.

Ideell gass

En ideell gass er en gass hvis partikler anses å være materielle punkter, det vil si at de ikke har dimensjoner, men har masse, og hvor all indre energi utelukkende består av den kinetiske energien til molekylers bevegelse og atomer.

Enhver ekte gass vil ideelt sett aldri tilfredsstille den beskrevne modellen, siden partiklene fortsatt har noen lineære dimensjoner og samhandler med hverandre ved å bruke svake van der Waals-bindinger eller kjemiske bindinger av en annen type. Ved lave trykk og høye temperaturer er imidlertid avstandene mellom molekylene store, og deres kinetiske energi overstiger den potensielle energien dusinvis av ganger. Alt dette gjør det mulig å bruke med høy grad av nøyaktighet den ideelle modellen for ekte gasser.

Intern energi av gass

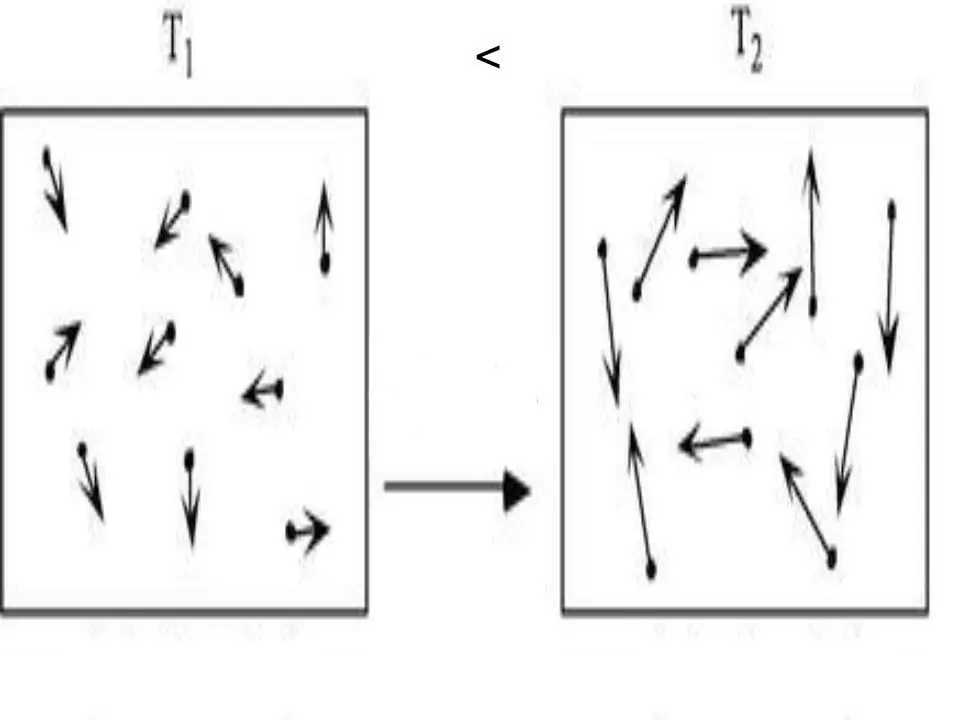
Den indre energien til ethvert system er en fysisk egenskap, som er lik summen av potensiell og kinetisk energi. Siden potensiell energi kan neglisjeres i ideelle gasser, kan vi skrive likheten for dem:

U=E_k.

Hvor E_k er energien til det kinetiske systemet. Ved å bruke den molekylære kinetiske teorien og anvende den universelle Clapeyron-Mendeleev tilstandsligningen, er det ikke vanskelig å få et uttrykk for U. Det er skrevet nedenfor:

U=z/2nRT.

Her er T, R og n henholdsvis den absolutte temperaturen, gasskonstanten og stoffmengden. Z-verdien er et heltall som indikerer antall frihetsgrader et gassmolekyl har.

Isobarisk og isokorisk varmekapasitet

I fysikk er varmekapasitet mengden varme som må tilføres systemet som studeres for å varme det opp med én kelvin. Den omvendte definisjonen er også sant, det vil si at varmekapasiteten er mengden varme som systemet avgir når det avkjøles med én kelvin.

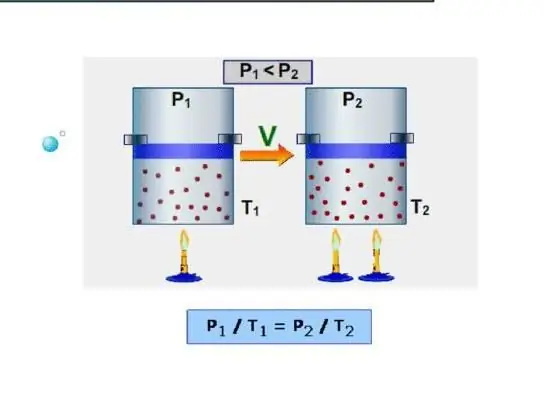
Den enkleste måten for et system er å bestemme den isokoriske varmekapasiteten. Det forstås som varmekapasiteten ved konstant volum. Siden systemet ikke utfører arbeid under slike forhold, brukes all energi på å øke interne energireserver. La oss betegne den isokoriske varmekapasiteten med symbolet C_V, så kan vi skrive:

dU=C_VdT.

Det vil si endringen i indre energisystemet er direkte proporsjon alt med endringen i temperaturen. Hvis vi sammenligner dette uttrykket med likheten skrevet i forrige avsnitt, kommer vi til formelen for C_V i en ideell gass:

С_V=z/2nR.

Denne verdien er upraktisk å bruke i praksis, siden den avhenger av mengden stoff i systemet. Derfor ble konseptet med spesifikk isokorisk varmekapasitet introdusert, det vil si en verdi som beregnes enten per 1 mol gass eller per 1 kg. La oss angi den første verdien med symbolet C_V, den andre - med symbolet C_V m^{. For dem kan du skrive følgende formler:}

C_V=z/2R;

C_V^m=z/2R/M.

Her er M den molare massen.

Isobar er varmekapasiteten samtidig som den opprettholder et konstant trykk i systemet. Et eksempel på en slik prosess er ekspansjonen av gass i en sylinder under et stempel når den varmes opp. I motsetning til den isokoriske prosessen, under den isobariske prosessen, brukes varmen som tilføres systemet til å øke den indre energien og utføre mekanisk arbeid, det vil si:

H=dU + PdV.

Entalpien til en isobar prosess er produktet av den isobariske varmekapasiteten og endringen i temperaturen i systemet, det vil si:

H=C_PdT.

Hvis vi vurderer ekspansjonen ved et konstant trykk på 1 mol gass, vil termodynamikkens første lov skrives som:

C_PdT=C_V dT + RdT.

Siste ledd er hentet fra ligningenClapeyron-Mendeleev. Fra denne likheten følger forholdet mellom isobariske og isokoriske varmekapasiteter:

C_P=C_V + R.

For en ideell gass er den spesifikke molare varmekapasiteten ved konstant trykk alltid større enn den tilsvarende isokoriske karakteristikk med R=8, 314 J/(molK).

Frihetsgrader for molekyler og varmekapasitet

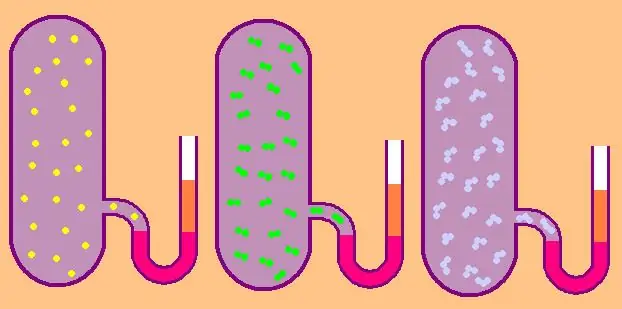
La oss skrive igjen formelen for den spesifikke molare isokoriske varmekapasiteten:

C_V=z/2R.

Når det gjelder en monoatomisk gass, er verdien z=3, siden atomer i rommet bare kan bevege seg i tre uavhengige retninger.

Hvis vi snakker om en gass som består av diatomiske molekyler, for eksempel oksygen O₂ eller hydrogen H₂, så, i tillegg til translasjonsbevegelse, kan disse molekylene fortsatt rotere rundt to innbyrdes perpendikulære akser, det vil si at z vil være lik 5.

For mer komplekse molekyler, bruk z=6. _{for å bestemme C}V