Naturfenomenene og prosessene rundt oss er ganske komplekse. For deres nøyaktige fysiske beskrivelse bør et tungvint matematisk apparat brukes og et stort antall vesentlige faktorer bør tas i betraktning. For å unngå dette problemet, brukes noen forenklede modeller i fysikk, som i stor grad letter den matematiske analysen av prosessen, men praktisk t alt ikke påvirker nøyaktigheten av beskrivelsen. En av dem er den ideelle gassmodellen. La oss vurdere det mer detaljert i artikkelen.
Konseptet med en ideell gass
En ideell gass er en tilstand av aggregering av et stoff, som består av materielle punkter som ikke samhandler med hverandre. La oss forklare denne definisjonen mer detaljert.
For det første snakker vi om materielle punkter som objekter som utgjør en ideell gass. Dette betyr at dens molekyler og atomer ikke har en størrelse, men har en viss masse. Det er dristigen tilnærming kan gjøres ved å ta hensyn til det faktum at i alle virkelige gasser ved lave trykk og høye temperaturer, er avstanden mellom molekylene mye større enn deres lineære dimensjoner.
For det andre bør ikke molekylene i en ideell gass samhandle med hverandre. I virkeligheten eksisterer slike interaksjoner alltid. Så selv atomer av edelgasser opplever dipol-dipol-attraksjon. Med andre ord er van der Waals-interaksjoner til stede. Sammenlignet med den kinetiske energien til rotasjon og translasjonsbevegelse av molekyler, er imidlertid disse interaksjonene så små at de ikke påvirker egenskapene til gasser. Derfor kan de ikke vurderes når man løser praktiske problemer.
Det er viktig å merke seg at ikke alle gasser der tettheten er lav og temperaturen er høy kan anses som ideelle. I tillegg til van der Waals-interaksjoner finnes det andre, sterkere typer bindinger, for eksempel hydrogenbindinger mellom H2O-molekyler, som fører til et grovt brudd på gassidealitetsbetingelsene. Av denne grunn er ikke vanndamp en ideell gass, men luft er det.
Fysisk modell av en ideell gass
Denne modellen kan representeres som følger: anta at gasssystemet inneholder N partikler. Disse kan være atomer og molekyler av ulike kjemikalier og grunnstoffer. Antallet N-partikler er stort, så enheten "mol" brukes vanligvis for å beskrive det (1 mol tilsvarer Avogadros tall). De beveger seg alle i et eller annet volum V. Partikkelbevegelserer kaotiske og uavhengige av hverandre. Hver av dem har en viss hastighet v og beveger seg langs en rett bane.
Teoretisk sett er sannsynligheten for kollisjon mellom partikler nesten null, siden størrelsen deres er liten sammenlignet med avstandene mellom partikler. Men hvis en slik kollisjon oppstår, er den absolutt elastisk. I sistnevnte tilfelle bevares den totale bevegelsen til partiklene og deres kinetiske energi.
Den vurderte modellen av ideelle gasser er et klassisk system med et stort antall elementer. Derfor følger hastigheten og energien til partikler i den den statistiske fordelingen til Maxwell-Boltzmann. Noen partikler har lave hastigheter, mens andre har høye hastigheter. I dette tilfellet er det en viss smal fartsgrense, der de mest sannsynlige verdiene av denne mengden ligger. Hastighetsfordelingen til nitrogenmolekyler er vist skjematisk nedenfor.
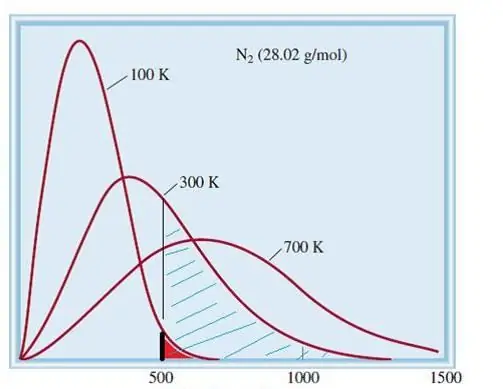
Kinetisk teori om gasser
Modellen av ideelle gasser beskrevet ovenfor bestemmer unikt egenskapene til gasser. Denne modellen ble først foreslått av Daniel Bernoulli i 1738.

Deretter ble den utviklet til sin nåværende tilstand av August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski og andre forskere.
Den kinetiske teorien om flytende stoffer, som den ideelle gassmodellen er bygget på, forklarer to viktige makroskopiske egenskaper til systemet basert på dets mikroskopiske oppførsel:
- Trykket i gasser er et resultat av kollisjonen av partikler med veggene i fartøyet.
- Temperaturen i systemet er et resultat av manifestasjonen av konstant bevegelse av molekyler og atomer.
La oss utvide begge konklusjonene til den kinetiske teorien.
Gasspress
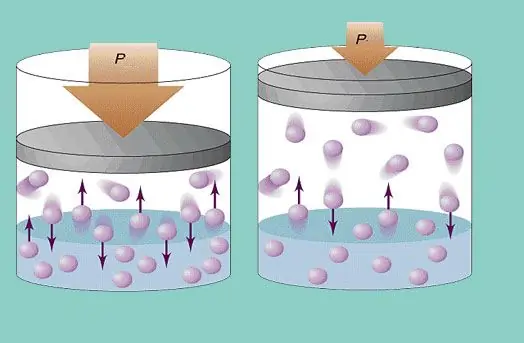
Den ideelle gassmodellen forutsetter en konstant kaotisk bevegelse av partikler i systemet og deres konstante kollisjon med fartøyets vegger. Hver slik kollisjon anses som absolutt elastisk. Partikkelmassen er liten (≈10-27-10-25 kg). Derfor kan den ikke skape mye trykk i en kollisjon. Likevel er antallet partikler, og dermed antallet kollisjoner, enormt (≈1023). I tillegg er grunnmiddelhastigheten til grunnstoffene flere hundre meter per sekund ved romtemperatur. Alt dette fører til dannelsen av et betydelig trykk på fartøyets vegger. Den kan beregnes ved hjelp av følgende formel:
P=Nmvcp2 / (3V), der vcp er rotens gjennomsnittlige kvadrathastighet, m er partikkelmasse.
Absolutt temperatur
I henhold til den ideelle gassmodellen er temperaturen unikt bestemt av den gjennomsnittlige kinetiske energien til et molekyl eller atom i systemet som studeres. Du kan skrive følgende uttrykk som relaterer kinetisk energi og absolutt temperatur for en ideell gass:
mvcp2 / 2=3 / 2kB T.
Her er kB Boltzmann-konstanten. Fra denne likheten får vi:
T=m vcp2 / (3kB).
Universell tilstandsligning
Hvis vi kombinerer uttrykkene ovenfor for absolutt trykk P og absolutt temperatur T, kan vi skrive følgende likhet:
PV=nRT.
Her er n mengden stoff i mol, R er gasskonstanten introdusert av D. I. Mendeleev. Dette uttrykket er den viktigste ligningen i teorien om ideelle gasser, fordi det kombinerer tre termodynamiske parametere (V, P, T) og ikke er avhengig av de kjemiske egenskapene til gasssystemet.

Den universelle ligningen ble først eksperimentelt utledet av den franske fysikeren Emile Clapeyron på 1800-tallet og deretter brakt til sin moderne form av den russiske kjemikeren Mendeleev, og det er derfor den for tiden bærer navnene til disse forskerne.






