Hver person i løpet av livet møter kropper som er i en av de tre aggregerte materietilstandene. Den enkleste aggregeringstilstanden å studere er gass. I artikkelen vil vi vurdere konseptet med en ideell gass, gi systemets tilstandsligning, og også være oppmerksom på beskrivelsen av den absolutte temperaturen.
Gasstilstand
Hver elev har en god ide om hvilken materietilstand de snakker om når de hører ordet "gass". Dette ordet forstås som en kropp som er i stand til å okkupere et hvilket som helst volum gitt til det. Den er ikke i stand til å holde formen sin, fordi den ikke kan motstå selv den minste ytre påvirkning. Gass holder heller ikke på volum, noe som skiller den ikke bare fra faste stoffer, men også fra væsker.
Som en væske er en gass et flytende stoff. I prosessen med bevegelse av faste kropper i gasser, hindrer sistnevnte denne bevegelsen. Den resulterende kraften kalles motstand. Verdien avhenger avhastigheten til kroppen i gassen.
Sterke eksempler på gasser er luft, naturgass som brukes til oppvarming av boliger og matlaging, inerte gasser (Ne, Ar) som brukes til å fylle reklamegløderør eller brukes til å skape et inert (ikke-aggressivt, beskyttende) miljø ved sveising.
Ideell gass
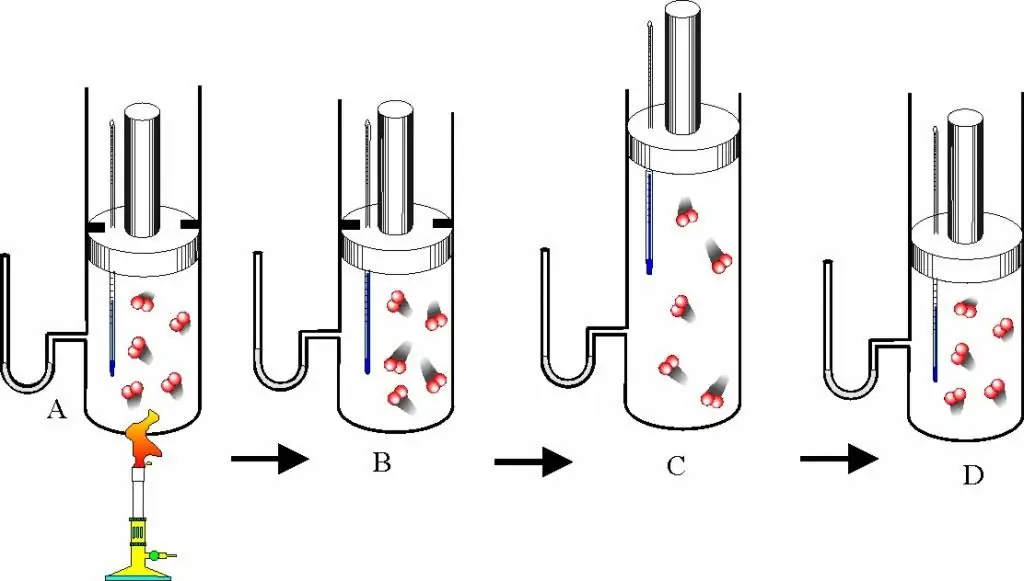
Før du går videre til beskrivelsen av gasslover og tilstandsligningen, bør du forstå spørsmålet om hva en ideell gass er. Dette konseptet er introdusert i molekylær kinetisk teori (MKT). En ideell gass er enhver gass som tilfredsstiller følgende egenskaper:
- Partiklerne som danner det, samhandler ikke med hverandre bortsett fra direkte mekaniske kollisjoner.
- Som et resultat av kollisjonen av partikler med fartøyets vegger eller mellom seg, bevares deres kinetiske energi og momentum, det vil si at kollisjonen anses som absolutt elastisk.
- Partikler har ingen dimensjoner, men har en endelig masse, det vil si at de ligner på materialpunkter.
Det er naturlig at enhver gass ikke er ideell, men ekte. Ikke desto mindre, for å løse mange praktiske problemer, er disse tilnærmingene ganske gyldige og kan brukes. Det er en generell empirisk regel som sier: uavhengig av kjemisk natur, hvis en gass har en temperatur over romtemperatur og et trykk i størrelsesorden atmosfærisk eller lavere, så kan den betraktes som ideell med høy nøyaktighet og kan brukes til å beskrive den.formel for den ideelle gassligningen for tilstand.
Clapeyron-Mendeleev lov
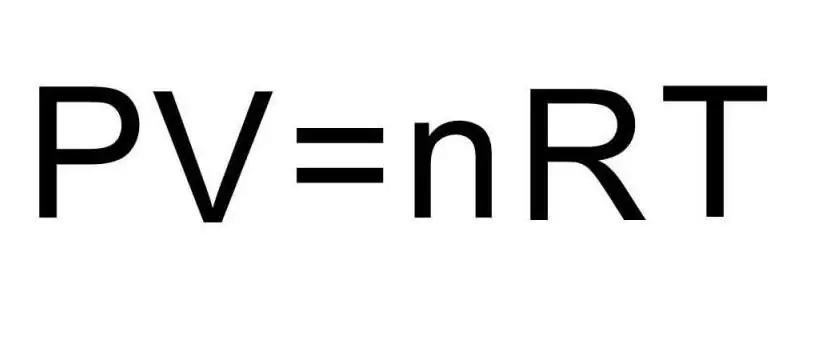
Overganger mellom ulike aggregerte tilstander av materie og prosesser innenfor en enkelt aggregert tilstand håndteres av termodynamikk. Trykk, temperatur og volum er tre størrelser som unikt definerer enhver tilstand i et termodynamisk system. Formelen for tilstandsligningen til en ideell gass kombinerer alle tre av disse mengdene til en enkelt likhet. La oss skrive denne formelen:
PV=nRT
Her P, V, T - henholdsvis trykk, volum, temperatur. Verdien av n er mengden stoff i mol, og symbolet R angir den universelle konstanten til gasser. Denne likheten viser at jo større produkt av trykk og volum er, desto større må produktet av stoffmengde og temperatur være.

Formelen for tilstandsligningen til en gass kalles Clapeyron-Mendeleev-loven. I 1834 kom den franske forskeren Emile Clapeyron, som oppsummerte de eksperimentelle resultatene til sine forgjengere, til denne ligningen. Imidlertid brukte Clapeyron en rekke konstanter, som Mendeleev senere erstattet med en - den universelle gasskonstanten R (8, 314 J / (molK)). Derfor, i moderne fysikk, er denne ligningen oppk alt etter navnene på franske og russiske forskere.

Andre ligningsskjemaer
Ovenfor skrev vi Mendeleev-Clapeyron-statsligningen for en ideell gass i det generelt aksepterte ogpraktisk form. Men i problemer innen termodynamikk kan det ofte være nødvendig med en litt annen form. Tre flere formler er skrevet nedenfor, som følger direkte av den skrevne ligningen:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Disse tre ligningene er også universelle for en ideell gass, bare i dem oppstår slike mengder som masse m, molar masse M, tetthet ρ og antall partikler N som utgjør systemet. Symbolet kB her angir Boltzmann-konstanten (1, 3810-23J/K).
Boyle-Mariotte Law
Da Clapeyron utarbeidet ligningen sin, var han basert på gasslover som var blitt oppdaget eksperimentelt flere tiår tidligere. En av dem er Boyle-Mariotte-loven. Det gjenspeiler en isoterm prosess i et lukket system, som et resultat av at slike makroskopiske parametere som trykk og volum endres. Hvis vi setter T og n konstant i tilstandsligningen for en ideell gass, vil gassloven ha formen:
P1V1=P2V 2
Dette er Boyle-Mariotte-loven, som sier at produktet av trykk og volum bevares under en vilkårlig isoterm prosess. I dette tilfellet endres selve verdiene P og V.
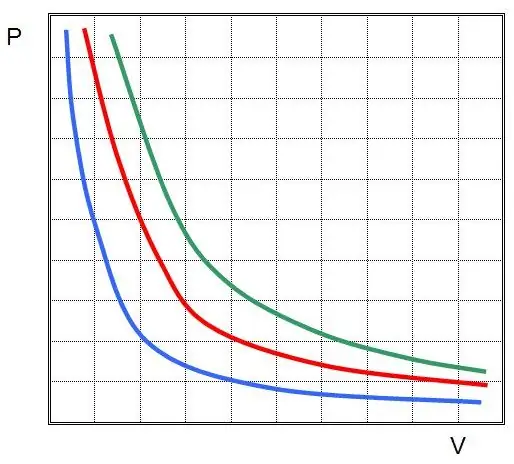
Hvis du plotter P(V) eller V(P), vil isotermene være hyperbler.
Charles og Gay-Lussacs lover
Disse lovene beskriver matematisk isobarisk og isokoriskprosesser, det vil si slike overganger mellom gasssystemets tilstander, der henholdsvis trykk og volum bevares. Charles' lov kan skrives matematisk som følger:
V/T=const når n, P=const.
Gay-Lussacs lov er skrevet som følger:
P/T=const når n, V=const.
Hvis begge likhetene presenteres i form av en graf, vil vi få rette linjer som er skråstilt i en eller annen vinkel til x-aksen. Denne typen grafer indikerer en direkte proporsjonalitet mellom volum og temperatur ved konstant trykk og mellom trykk og temperatur ved konstant volum.
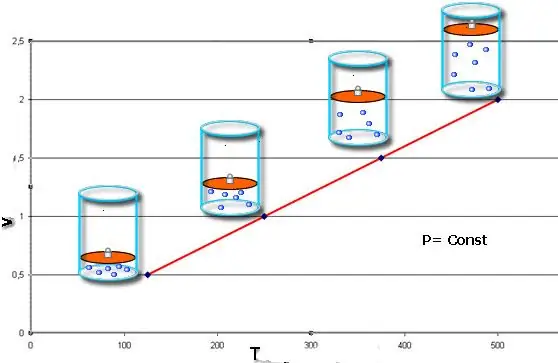
Merk at alle de tre betraktede gasslovene ikke tar hensyn til den kjemiske sammensetningen av gassen, så vel som endringen i dens mengde stoff.
Absolutt temperatur
I hverdagen er vi vant til å bruke Celsius-temperaturskalaen, siden den er praktisk for å beskrive prosessene rundt oss. Så vannet koker ved 100 oC og fryser ved 0 oC. I fysikk viser denne skalaen seg å være upraktisk, derfor brukes den såk alte absolutte temperaturskalaen, som ble introdusert av Lord Kelvin på midten av 1800-tallet. I henhold til denne skalaen måles temperaturen i Kelvin (K).
Det antas at ved en temperatur på -273, 15 oC er det ingen termiske vibrasjoner av atomer og molekyler, deres foroverbevegelse stopper helt. Denne temperaturen i grader Celsius tilsvarer absolutt null i Kelvin (0 K). Fra denne definisjonenden fysiske betydningen av absolutt temperatur følger: det er et mål på den kinetiske energien til partiklene som utgjør stoffet, for eksempel atomer eller molekyler.
I tillegg til ovennevnte fysiske betydning av absolutt temperatur, er det andre tilnærminger til å forstå denne mengden. En av dem er den nevnte gassloven til Charles. La oss skrive det i følgende form:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Den siste likheten sier at ved en viss mengde stoff i systemet (for eksempel 1 mol) og et visst trykk (for eksempel 1 Pa), bestemmer gassvolumet unikt den absolutte temperaturen. Med andre ord, en økning i gassvolumet under disse forholdene er kun mulig på grunn av en temperaturøkning, og en reduksjon i volum indikerer en reduksjon i verdien av T.
Husk at, i motsetning til Celsius-temperatur, kan absolutt temperatur ikke være negativ.
Avogadro-prinsippet og gassblandinger
I tillegg til de ovennevnte gasslovene, fører tilstandsligningen for en ideell gass også til prinsippet som ble oppdaget av Amedeo Avogadro på begynnelsen av 1800-tallet, og som bærer etternavnet hans. Dette prinsippet fastslår at volumet av enhver gass ved konstant trykk og temperatur bestemmes av mengden stoff i systemet. Den tilsvarende formelen ser slik ut:
n/V=const når P, T=const.
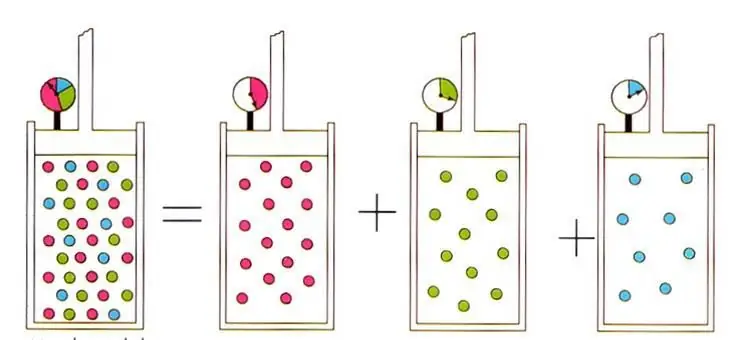
Det skriftlige uttrykket fører til den velkjente innen ideell gassfysikk D altons lov for gassblandinger. Detteloven sier at parti altrykket til en gass i en blanding er unikt bestemt av dens atomfraksjon.
Eksempel på problemløsning
I et lukket kar med stive vegger som inneholder en ideell gass, økte trykket 3 ganger som følge av oppvarming. Det er nødvendig å bestemme den endelige temperaturen til systemet hvis startverdien var 25 oC.
Først, la oss konvertere temperaturen fra grader Celsius til Kelvin, vi har:
T=25 + 273, 15=298, 15 K.
Siden veggene i karet er stive, kan oppvarmingsprosessen betraktes som isokorisk. For dette tilfellet bruker vi Gay-Lussac-loven, vi har:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Dermed bestemmes slutttemperaturen fra produktet av trykkforholdet og starttemperaturen. Ved å erstatte dataene med likhet, får vi svaret: T2=894,45 K. Denne temperaturen tilsvarer 621,3 oC.






