Som du vet, tilhører enhver fysisk mengde en av to typer, den er enten skalar eller vektor. I denne artikkelen vil vi ta for oss kinematiske egenskaper som hastighet og akselerasjon, og også vise hvor akselerasjons- og hastighetsvektorene er rettet.
Hva er hastighet og akselerasjon?
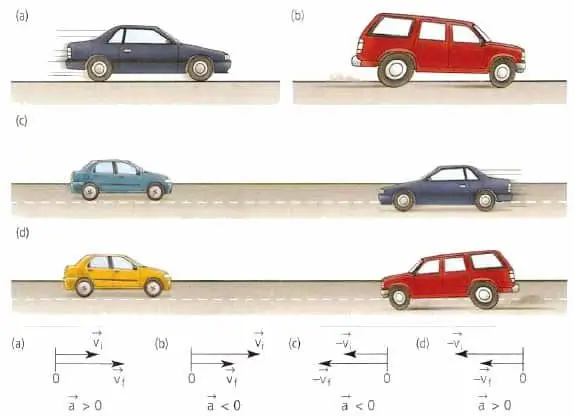
Begge mengdene nevnt i dette avsnittet er viktige kjennetegn ved enhver form for bevegelse, enten det er å bevege en kropp i en rett linje eller langs en buet bane.
Speed er hastigheten som koordinatene endres med over tid. Matematisk er denne verdien lik den tidsderiverte av tilbakelagt distanse, det vil si:
v¯=dl¯/dt.
Her er vektoren l¯ rettet fra startpunktet på banen til sluttpunktet.
I sin tur er akselerasjon hastigheten som selve hastigheten endrer seg med over tid. I form av en formel kan den skrives slik:
a¯=dv¯/dt.
Åpenbart, tar den andre deriverte avforskyvningsvektor l¯ med tiden, vil vi også få verdien av akselerasjonen.
Siden hastighet måles i meter per sekund, måles akselerasjon, i henhold til det skriftlige uttrykket, i meter per sekund i kvadrat.

Hvor er akselerasjons- og hastighetsvektorene?
I fysikk er enhver mekanisk bevegelse av en kropp vanligvis preget av en bestemt bane. Sistnevnte er en imaginær kurve som kroppen beveger seg langs i rommet. For eksempel er en rett linje eller en sirkel gode eksempler på vanlige bevegelsesbaner.
Kroppens hastighetsvektor er alltid rettet i bevegelsesretningen, uavhengig av om kroppen bremser ned eller akselererer, om den beveger seg i en rett linje eller langs en kurve. Når vi snakker i geometriske termer, er hastighetsvektoren rettet tangentielt til punktet på banen der kroppen befinner seg for øyeblikket.
Akselerasjonsvektoren til et materiale eller kroppspunkt har ingenting med hastighet å gjøre. Denne vektoren er rettet i retning av hastighetsendring. For eksempel, for rettlinjet bevegelse, kan verdien a¯ enten falle sammen i retning med v¯ eller være motsatt av v¯.
Tving som virker på kroppen og akselerasjon
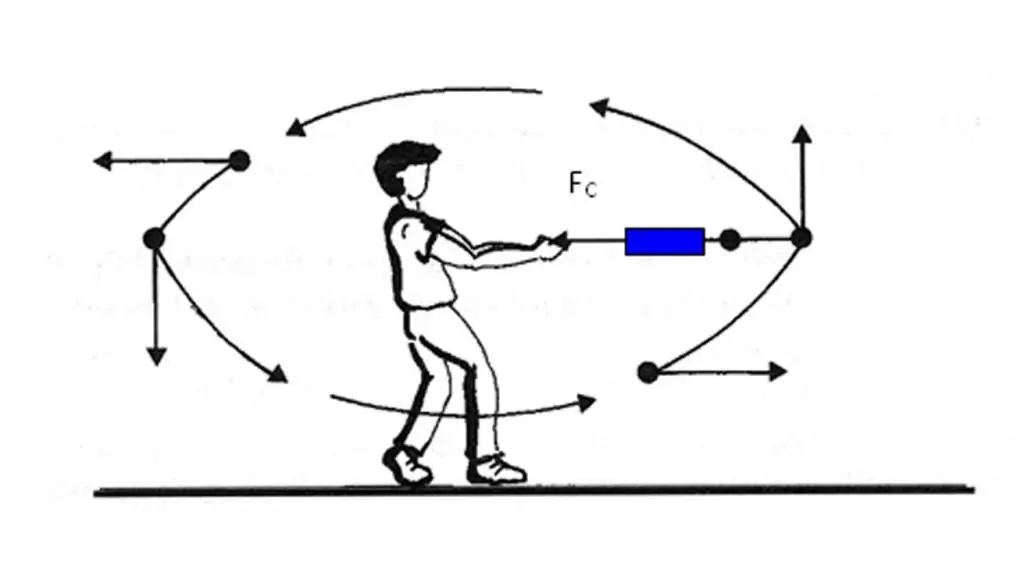
Vi har funnet ut at akselerasjonsvektoren til kroppen er rettet mot endringen av hastighetsvektoren. Det er imidlertid ikke alltid lett å fastslå hvordan hastigheten endres på et gitt punkt i banen. Dessuten, for å bestemme endringen i hastighet, er det nødvendig å utføre operasjonenvektorforskjeller. For å unngå disse vanskelighetene med å bestemme retningen til vektoren a¯, er det en annen måte å finne ut av det raskt.
Nedenfor er Newtons berømte og velkjente lov for alle studenter:
F¯=ma¯.
Formelen viser at årsaken til akselerasjon i kropper er kraften som virker på dem. Siden massen m er en skalar, er kraftvektoren F¯ og akselerasjonsvektoren a¯ i samme retning. Dette faktum bør huskes og brukes i praksis når det er behov for å bestemme retningen til mengden a¯.
Hvis flere forskjellige krefter virker på kroppen, vil retningen til akselerasjonsvektoren være lik den resulterende vektoren av alle krefter.
Sirkulær bevegelse og akselerasjon
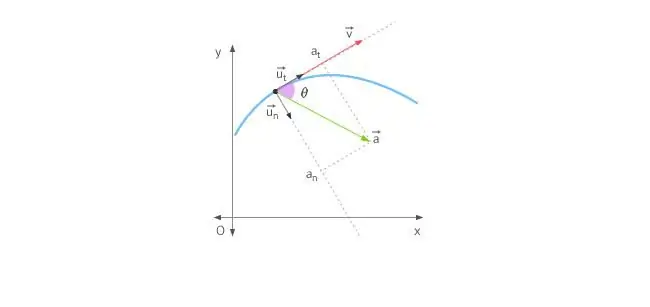
Når en kropp beveger seg i en rett linje, rettes akselerasjonen enten fremover eller bakover. Ved bevegelse i en sirkel kompliseres situasjonen av at hastighetsvektoren hele tiden endrer retning. I lys av ovenstående bestemmes den totale akselerasjonen av de to komponentene: tangentiell og normal akselerasjon.
Tangensiell akselerasjon er rettet nøyaktig det samme som hastighetsvektoren, eller mot den. Med andre ord er denne akselerasjonskomponenten rettet langs tangenten til banen. Tangentiell akselerasjon beskriver endringen i modulen til selve hastigheten.
Normal akselerasjon rettes langs normalen til det gitte punktet i banen, tatt i betraktning krumningen. Ved sirkulær bevegelse indikerer vektoren til denne komponententil sentrum, det vil si at den normale akselerasjonen er rettet langs rotasjonsradiusen. Denne komponenten kalles ofte centripetal.
Fullakselerasjon er summen av disse komponentene, så vektoren kan rettes vilkårlig i forhold til sirkellinjen.
Hvis kroppen roterer uten å endre den lineære hastigheten, er det bare en normalkomponent som ikke er null, så fullakselerasjonsvektoren er rettet mot sentrum av sirkelen. Merk at dette senteret også påvirkes av en kraft som holder kroppen på banen. For eksempel holder gravitasjonskraften til solen jorden vår og andre planeter i deres baner.






