Naturlige geometriske mønstre eller mønstre vises som repeterende former som noen ganger kan beskrives eller representeres av matematiske modeller.
Geometri i naturen og livet kommer i mange former og former, for eksempel symmetri, spiraler eller bølger.
Historie
For første gang tok antikke greske filosofer og vitenskapsmenn - Pythagoras, Empedocles og Platon - opp spørsmål om geometri i naturen. Ved å analysere eksempler på forutsigbare eller ideelle geometriske former hos planter og dyr forsøkte de å demonstrere orden og symmetri i naturen.
Moderne forsøk på å studere geometri i naturen begynte på 1800-tallet med innsatsen til den belgiske fysikeren Joseph Plateau, som utviklet konseptet om minimumsoverflaten til en såpeboble. De første moderne forsøkene konsentrerte seg først om å demonstrere ideelle og forutsigbare geometriske former, og deretter vendte de seg mot utviklingen av modeller som forutsier utseendet og manifestasjonen av geometri i naturen.
På 1900-tallet arbeidet matematiker Alan Turing med mekanismene for morfogenese, som forklarer utseendet hos dyrulike mønstre, striper, flekker. Litt senere skal biologen Aristide Lindenmeier sammen med matematikeren Benoit Mandelbrot fullføre arbeidet med matematiske fraktaler som gjentok vekstmønstrene til enkelte planter, inkludert trær.
Vitenskap
Moderne vitenskaper (matematikk, fysikk og kjemi), ved hjelp av teknologier og modeller, prøver ikke bare å forklare, men også å forutsi de geometriske mønstrene som finnes i naturen.
Formen og fargen til mange levende organismer, som påfugl, kolibrier og skjell, er ikke bare vakre, men også geometrisk korrekte, noe som tiltrekker forskernes nysgjerrighet. Skjønnheten vi observerer i naturen kan forårsakes naturlig, matematisk.
De observerte naturlige mønstrene i matematikk forklares av kaosteori, som fungerer med spiraler og fraktaler. Slike mønstre adlyder fysikkens lover, i tillegg forutsier fysikk og kjemi, ved hjelp av abstrakt matematikk, formene til krystaller, både naturlige og kunstige.
Biologi forklarer geometrien i naturen ved naturlig utvalg, der slike vanlige egenskaper som striper, flekker, lyse farger kan forklares med behovet for maskering eller å sende signaler.
Typer of patterns
I naturen er det mange gjentakende mønstre som vises i ulike geometriske former. Typer av grunnleggende regelmessigheter for geometri i naturen, bilder og deres beskrivelser finner du nedenfor.
Symmetri. Denne geometriske formen er en av de vanligste i naturen. Mest vanlig hos dyrspeilsymmetri - sommerfugler, biller, tigre, ugler. Den finnes også i planter, som lønneblader eller orkideblomster. I tillegg kan symmetrisk geometri i naturen være radial, femstrålende eller seksdobbel, som snøfnugg.

Fraktaler. I matematikk er dette selvliknende konstruksjoner som er uendelige. I naturen er det umulig å oppdage en slik endeløs selvrepeterende form, derfor kalles tilnærminger av fraktale mønstre geometriske fraktaler i naturen. Slik geometri kan observeres i naturen i bregneblader, brokkoli, ananasfrukter.
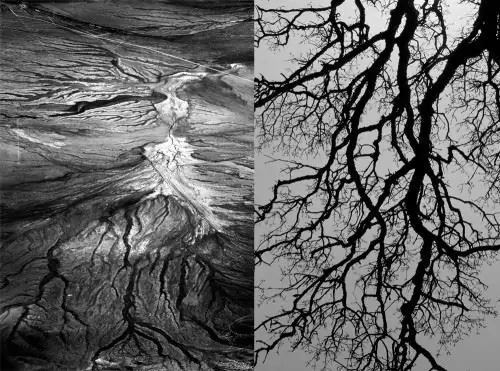
Spiraler. Disse formene er spesielt vanlige blant bløtdyr og snegler. Forskere observerer spiralformer i verdensrommet, for eksempel spiralgalakser. Spiralen kalles Fibonaccis gyldne snitt.

Meanders. Tilfeldigheten til dynamiske systemer i matematikk manifesterer seg i naturen i slike former som bukter og flyter. Naturlig geometri har form av en brutt eller snarere buet linje, for eksempel en elvestrøm.
Bølger. De er forårsaket av forstyrrelser og bevegelser av luft, vindstrømmer, spredt både gjennom luft og gjennom vann. I naturen er dette ikke bare havbølger, men også ørkendyner, som kan danne geometriske former - linjer, halvmåner og paraboler.
mosaikk. Laget ved å gjenta de samme elementene på overflaten. Mosaikkgeometri i dyrelivet finnes hos bier: de byggerbikube av honningkaker - repeterende celler.

Formasjon av mønstre
I biologi skyldes dannelsen av en geometrisk farge prosessen med naturlig utvalg. Tilbake på midten av 1900-tallet klarte Alan Turing å beskrive mekanismen for oppkomsten av flekker og striper i fargen på dyr - han k alte det reaksjonsdiffusjonsmodellen. Enkelte celler i kroppen inneholder gener som styres av kjemiske reaksjoner. Morfogen fører til dannelse av hudområder med mørkt pigment (flekker og striper). Hvis morfogenet er tilstede i alle hudceller - fargen på panteren oppnås, hvis den er ujevnt tilstede - den vanlige flekkleoparden.






