Komplekse tall: definisjon og grunnleggende begreper

2024 Forfatter: Angel Austin | [email protected]. Sist endret: 2023-12-17 05:37

Når man studerer egenskapene til en kvadratisk ligning, ble det satt en begrensning - for en diskriminant mindre enn null er det ingen løsning. Det ble umiddelbart fastsatt at vi snakker om et sett med reelle tall. Det nysgjerrige sinnet til en matematiker vil være interessert - hva er hemmeligheten i klausulen om virkelige verdier?

Over tid introduserte matematikere konseptet komplekse tall, der den betingede verdien av den andre roten av minus én tas som en enhet.

Historisk bakgrunn

Matematisk teori utvikler seg sekvensielt, fra enkel til kompleks. La oss finne ut hvordan konseptet k alt "komplekst tall" oppsto og hvorfor det er nødvendig.

Fra uminnelige tider var grunnlaget for matematikk den vanlige beretningen. Forskerne kjente bare til det naturlige verdisettet. Addisjon og subtraksjon var enkel. Etter hvert som økonomiske relasjoner ble mer komplekse, begynte man å bruke multiplikasjon i stedet for å legge til de samme verdiene. Det er en omvendt operasjon tilmultiplikasjon - divisjon.

Konseptet med et naturlig tall begrenset bruken av aritmetiske operasjoner. Det er umulig å løse alle divisjonsproblemer på settet med heltallsverdier. Arbeid med brøker førte først til begrepet rasjonelle verdier, og deretter til irrasjonelle verdier. Hvis det for det rasjonelle er mulig å indikere den nøyaktige plasseringen av punktet på linjen, så er det for det irrasjonelle umulig å indikere et slikt punkt. Du kan bare beregne intervallet. Foreningen av rasjonelle og irrasjonelle tall dannet et reelt sett, som kan representeres som en viss linje med en gitt skala. Hvert trinn langs linjen er et naturlig tall, og mellom dem er det rasjonelle og irrasjonelle verdier.

Epoken med teoretisk matematikk har begynt. Utviklingen av astronomi, mekanikk, fysikk krevde løsning av flere og mer komplekse ligninger. Generelt ble røttene til den kvadratiske ligningen funnet. Da forskerne løste et mer komplekst kubisk polynom, møtte forskerne en selvmotsigelse. Konseptet med en terningrot fra en negativ gir mening, men for en kvadratrot oppnås usikkerhet. Dessuten er den kvadratiske ligningen bare et spesi altilfelle av den kubiske.

I 1545 foreslo italieneren J. Cardano å introdusere konseptet med et imaginært tall.

Dette tallet er den andre roten av minus én. Begrepet komplekst tall ble til slutt dannet bare tre hundre år senere, i verkene til den berømte matematikeren Gauss. Han foreslo formelt å utvide alle algebralovene til det imaginære tallet. Den virkelige linjen er utvidet tilfly. Verden er større.

Grunnleggende konsepter

Hent en rekke funksjoner som har begrensninger på det virkelige settet:

y=arcsin(x), definert mellom negativ og positiv 1.
y=ln(x), desimallogaritme gir mening med positive argumenter.
kvadratrot y=√x, beregnet kun for x ≧ 0.

Betegner i=√(-1), introduserer vi et slikt konsept som et imaginært tall, dette vil fjerne alle begrensninger fra definisjonsdomenet til funksjonene ovenfor. Uttrykk som y=arcsin(2), y=ln(-4), y=√(-5) gir mening i et rom med komplekse tall.

Den algebraiske formen kan skrives som et uttrykk z=x + i×y på settet med reelle x- og y-verdier, og i² =-1.

Det nye konseptet fjerner alle restriksjoner på bruken av enhver algebraisk funksjon og ligner en graf av en rett linje i koordinater av reelle og imaginære verdier.

komplekst fly

Den geometriske formen til komplekse tall tillater oss visuelt å representere mange av egenskapene deres. På Re(z)-aksen markerer vi de reelle x-verdiene, på Im(z) - de imaginære verdiene til y, så vil z-punktet på planet vise den nødvendige komplekse verdien.

geometrisk representasjon av et komplekst tall

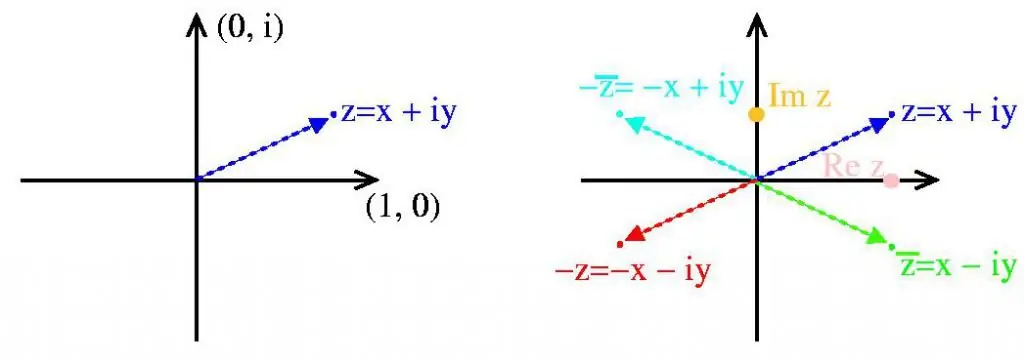
Definisjoner:

Re(z) - reell akse.
Im(z) - betyr den imaginære aksen.
z – betinget punkt i et komplekst tall.
Den numeriske verdien av lengden på vektoren fra null til z kallesmodul.
Ekte og imaginære akser deler flyet inn i kvartaler. Med en positiv verdi av koordinatene - jeg kvartal. Når argumentet til den reelle aksen er mindre enn 0, og den imaginære aksen er større enn 0 - II kvart. Når koordinatene er negative - III kvartal. Det siste, fjerde kvartalet inneholder mange positive reelle verdier og negative imaginære verdier.

På et plan med x- og y-koordinatverdier kan man altså alltid visualisere et punkt med et komplekst tall. Tegnet i er introdusert for å skille den virkelige delen fra den imaginære.

Properties

Når verdien av det imaginære argumentet er null, får vi bare et tall (z=x), som er plassert på den reelle aksen og tilhører den reelle mengden.
Spesi altilfelle når verdien av det reelle argumentet blir null, tilsvarer uttrykket z=i×y plasseringen av punktet på den imaginære aksen.
Den generelle formen for z=x + i×y vil være for verdier som ikke er null for argumentene. Indikerer plasseringen av punktet som karakteriserer det komplekse tallet i ett av kvartalene.

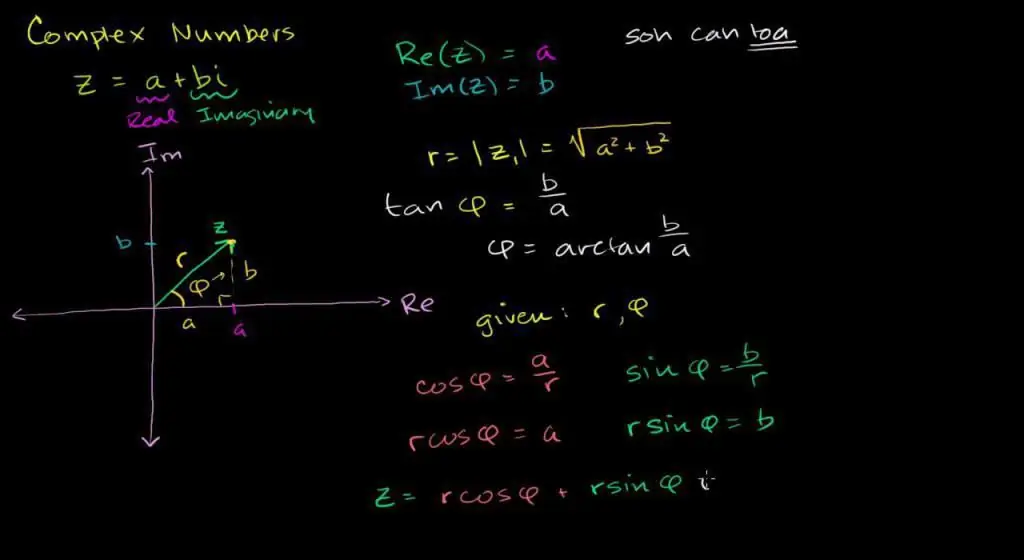
Trigonometrisk notasjon

Hent det polare koordinatsystemet og definisjonen av de trigonometriske funksjonene sin og cos. Det er åpenbart at ved hjelp av disse funksjonene er det mulig å beskrive plasseringen av et hvilket som helst punkt på flyet. For å gjøre dette er det nok å vite lengden på polarstrålen og helningsvinkelen til den reelle aksen.

Definisjon. En oppføring på formen ∣z ∣ multiplisert med summen av de trigonometriske funksjonene cos(ϴ) og den imaginære delen i ×sin(ϴ) kalles et trigonometrisk komplekst tall. Her er betegnelsen helningsvinkelen til den reelle aksen

ϴ=arg(z) og r=∣z∣, strålelengde.

Fra definisjonen og egenskapene til trigonometriske funksjoner følger en veldig viktig Moivre-formel:

zⁿ =r × (cos(n × ϴ) + i × sin(n × ϴ)).

Ved å bruke denne formelen er det praktisk å løse mange ligningssystemer som inneholder trigonometriske funksjoner. Spesielt når problemet med å heve til en makt oppstår.

Modul og fase

For å fullføre beskrivelsen av et komplekst sett foreslår vi to viktige definisjoner.

Når du kjenner Pythagoras teorem, er det enkelt å beregne lengden på strålen i det polare koordinatsystemet.

r=∣z∣=√(x² + y²), en slik notasjon på et komplekst rom kalles en " modul" og karakteriserer avstanden fra 0 til et punkt på flyet.

Helningsvinkelen til den komplekse strålen til den reelle linjen ϴ kalles vanligvis fasen.

Definisjonen viser at de reelle og imaginære delene er beskrevet ved hjelp av sykliske funksjoner. Nemlig:

x=r × cos(ϴ);
y=r × sin(ϴ);

Omvendt er fasen relatert til algebraiske verdier gjennom formelen:

ϴ=arctan(x / y) + µ, korreksjon µ er introdusert for å ta hensyn til periodisiteten til geometriske funksjoner.

Euler-formel

Matematikere bruker ofte eksponentiell form. Komplekse plantall skrives som uttrykk

z=r × eⁱ^×^ϴ , som følger av Euler-formelen.

Denne posten er mye brukt til praktisk beregning av fysiske mengder. Presentasjonsform i skjemaeteksponentielle komplekse tall er spesielt praktisk for tekniske beregninger, der det blir nødvendig å beregne kretsløp med sinusformede strømmer og det er nødvendig å kjenne verdien av integraler av funksjoner med en gitt periode. Selve beregningene fungerer som et verktøy i utformingen av ulike maskiner og mekanismer.

Definer operasjoner

Som allerede nevnt, gjelder alle algebraiske lover for arbeid med grunnleggende matematiske funksjoner for komplekse tall.

Sumoperasjon

Når du legger til komplekse verdier, legges også deres reelle og imaginære deler til.

z=z₁ + z₂ der z₁ og z2 _{- generelle komplekse tall. Ved å transformere uttrykket, etter å ha åpnet parentesene og forenklet notasjonen, får vi det reelle argumentet x=(x}1 _{+ x}2_{), det imaginære argumentet y=(y 1} + y₂).

På grafen ser det ut som addisjon av to vektorer, i henhold til den velkjente parallellogramregelen.

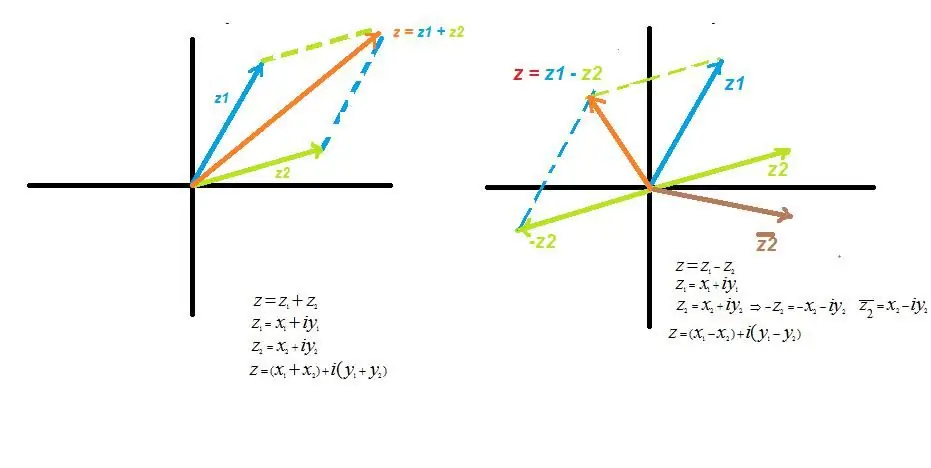
Subtraksjonsoperasjon

Betraktet som et spesielt tilfelle av addisjon, når ett tall er positivt, er det andre negativt, det vil si plassert i speilkvartalet. Algebraisk notasjon ser ut som forskjellen mellom ekte og imaginære deler.

z=z₁ - z₂, eller, tatt i betraktning verdiene til argumentene, på samme måte som tillegget operasjon, får vi for de reelle verdiene x=(x₁ - x₂) og imaginære y=(y₁- y₂).

Multiplikasjon på det komplekse planet

Ved å bruke reglene for arbeid med polynomer, utleder vi formelenfor å løse komplekse tall.

Følg de generelle algebraiske reglene z=z₁×z₂, beskriv hvert argument og skriv opp lignende. De virkelige og imaginære delene kan skrives slik:

x=x₁ × x₂ - y₁ × y₂,
y=x₁ × y₂ + x₂ × y _1.

Det ser vakrere ut hvis vi bruker eksponentielle komplekse tall.

Uttrykket ser slik ut: z=z₁ × z₂ =r₁ × eⁱ^ϴ¹ × r₂ × eiϴ2^=r1 _{× r2} × e_i(^ϴ¹⁺^ϴ2).

Enklere, modulene multipliseres og fasene legges til.

Division

Når vi betrakter operasjonen av divisjon som invers av multiplikasjon, får vi et enkelt uttrykk i eksponentiell notasjon. Å dele verdien z₁ med z₂ er resultatet av å dele modulene og faseforskjellen deres. Formelt, når du bruker eksponentiell form av komplekse tall, ser det slik ut:

z=z₁ / z₂ =r₁ × e ⁱ^ϴ¹ / r₂ × eⁱ ^ϴ²=r₁ / r_{2× e}i(ϴ1-ϴ 2).

I form av algebraisk notasjon er operasjonen med å dele tallene til det komplekse planet skrevet litt mer komplisert:

z=z₁ / z_2.

Beskriver argumenter og utfører polynomtransformasjoner, det er enkelt å få verdierx=x₁ × x₂ + y₁ × y₂, henholdsvis y=x₂ × y₁ - x₁ × y₂ , men innenfor det beskrevne rommet gir dette uttrykket mening hvis z₂ ≠ 0.

trekk ut roten

Alle de ovennevnte kan brukes når man definerer mer komplekse algebraiske funksjoner - heving til hvilken som helst potens og invers til den - ekstrahering av roten.

Ved å bruke det generelle konseptet med å heve til potensen n, får vi definisjonen:

zⁿ =(r × eⁱ^ϴ).

Bruk vanlige egenskaper, skriv om som:

zⁿ =rⁿ × eⁱ^ϴ.

Vi har en enkel formel for å heve et komplekst tall til en potens.

Fra definisjonen av graden får vi en svært viktig konsekvens. En jevn potens for den imaginære enheten er alltid 1. Enhver oddetall i den imaginære enheten er alltid -1.

La oss nå studere den inverse funksjonen - trekke ut roten.

For å lette notasjonen, la oss ta n=2. Kvadratroten w av den komplekse verdien z på det komplekse planet C anses å være uttrykket z=±, gyldig for ethvert reelt argument større enn eller lik null. For w ≦ 0 er det ingen løsning.

La oss se på den enkleste andregradsligningen z² =1. Bruk komplekse tallformler, omskriv r² × eⁱ^2ϴ =r² × eⁱ^2ϴ=ei0^{. Det kan sees fra posten at r}2 ^{=1 og ϴ=0, derfor har vi en unik løsning lik 1. Men dette motsier forestillingen om at z=-1 også passer til definisjonen av en kvadratrot.}

La oss finne ut hva vi ikke tar hensyn til. Hvis vi husker den trigonometriske notasjonen, gjenoppretter vi utsagnet - med en periodisk endring i fasen ϴ, endres ikke det komplekse tallet. La p betegne verdien av perioden, så har vi r² × eⁱ^2ϴ =ei(0+p)^{, hvorav 2ϴ=0 + p, eller ϴ=p / 2. Derfor, e}i0 ^{=1 og e}i^p^/2 =-1. Vi fikk den andre løsningen, som tilsvarer den generelle forståelsen av kvadratroten.

Så, for å finne en vilkårlig rot av et komplekst tall, følger vi prosedyren.

Skriv eksponentiell form w=∣w∣ × eⁱ⁽^arg (w) + pk), k er et vilkårlig heltall.
Det ønskede tallet er også representert i Euler-formen z=r × eⁱ^ϴ.
Bruk den generelle definisjonen av rotekstraksjonsfunksjonen r eⁱ ϴ ^{=∣w∣ × e}i(arg(w) + pk).
Fra de generelle egenskapene til likheten mellom moduler og argumenter skriver vi rⁿ =∣w∣ og nϴ=arg (w) + p×k.
Den siste posten av roten til et komplekst tall er beskrevet av formelen z=√∣w∣ × eⁱ ⁽ ^arg (w) + pk ^{) /} .
Merk. Verdien av ∣w∣, per definisjon,er et positivt reelt tall, så roten til enhver grad gir mening.

Felt og konjugasjon

Avslutningsvis gir vi to viktige definisjoner som er av liten betydning for å løse anvendte problemer med komplekse tall, men som er essensielle for den videre utviklingen av matematisk teori.

Uttrykkene for addisjon og multiplikasjon sies å danne et felt hvis de tilfredsstiller aksiomene for alle elementer i det komplekse planet z:

Den komplekse summen endres ikke fra å endre plassering av komplekse termer.
Utsagnet er sant – i et komplekst uttrykk kan enhver sum av to tall erstattes med verdien deres.
Det er en nøytral verdi 0 som z + 0=0 + z=z er sann for.
For enhver z er det en motsetning - z, som tillegg gir null.
Når du bytter plass til komplekse faktorer, endres ikke det komplekse produktet.
Multiplikasjonen av to vilkårlige tall kan erstattes med verdien deres.
Det er en nøytral verdi 1, multiplikasjon med som ikke endrer det komplekse tallet.
For hver z ≠ 0 er det en invers av z^-1, som multipliseres med 1.
Å multiplisere summen av to tall med en tredjedel tilsvarer operasjonen med å multiplisere hvert av dem med dette tallet og legge til resultatene.
0 ≠ 1.

Tallene z₁ =x + i×y og z₂ =x - i×y kalles konjugert.

Setning. For bøying er påstanden sann:

Bøyningen av summen er lik summen av konjugerte elementer.
Konjugatet til produktet erprodukt av konjugasjoner.
Bøyningen av bøying er lik selve tallet.

Generelt algebra kalles slike egenskaper feltautomorfismer.

Eksempler

Ved å følge de gitte reglene og formlene for komplekse tall, kan du enkelt bruke dem.

La oss vurdere de enkleste eksemplene.

Oppgave 1. Bruk ligningen 3y +5 x i=15 - 7i, bestem x og y.

Beslutning. Husk definisjonen av komplekse likheter, så 3y=15, 5x=-7. Derfor er x=-7 / 5, y=5.

Oppgave 2. Beregn verdiene 2 + i²⁸ og 1 + i¹³⁵.

Beslutning. Åpenbart er 28 et partall, fra konsekvensen av definisjonen av et komplekst tall i potensen har vi i²⁸ =1, som betyr at uttrykket 2 + i ²⁸ =3. Den andre verdien, i¹³⁵ =-1, deretter 1 + i¹³⁵ =0.

Oppgave 3. Regn ut produktet av verdiene 2 + 5i og 4 + 3i.

Beslutning. Fra de generelle egenskapene til multiplikasjon av komplekse tall får vi (2 + 5i)X(4 + 3i)=8 - 15 + i(6 + 20). Den nye verdien vil være -7 + 26i.

Oppgave 4. Regn ut røttene til ligningen z³ =-i.

Beslutning. Det er flere måter å finne et komplekst tall på. La oss vurdere en av de mulige. Per definisjon, ∣ - i∣=1, er fasen for -i -p / 4. Den opprinnelige ligningen kan skrives om som r³eⁱ3ϴ ^=e-p/4+pk^{, hvorfra z=e}-p / 12 + pk/3^{, for et heltall k.}

Løsningssettet har formen (e^-^ip/12,e^ip^/4, eⁱ² ^p/3).

Hvorfor trenger vi komplekse tall

Historien kjenner mange eksempler når forskere som arbeider med en teori, ikke engang tenker på den praktiske anvendelsen av resultatene deres. Matematikk er for det første et sinnsspill, en streng overholdelse av årsak-virkning-forhold. Nesten alle matematiske konstruksjoner er redusert til å løse integral- og differensialligninger, og de løses på sin side med en viss tilnærming ved å finne røttene til polynomer. Her møter vi først paradokset med imaginære tall.

Vitenskapsfolk som løser helt praktiske problemer, tyr til løsninger av forskjellige ligninger, oppdager matematiske paradokser. Tolkningen av disse paradoksene fører til helt fantastiske funn. Den doble naturen til elektromagnetiske bølger er et slikt eksempel. Komplekse tall spiller en avgjørende rolle for å forstå egenskapene deres.

Dette har i sin tur funnet praktisk anvendelse innen optikk, radioelektronikk, energi og mange andre teknologiske felt. Et annet eksempel, mye vanskeligere å forstå fysiske fenomener. Antimaterie ble spådd på tuppen av en penn. Og bare mange år senere begynner forsøk på å syntetisere den fysisk.

Ikke tenk at det er slike situasjoner bare i fysikk. Ikke mindre interessante funn gjøres i dyrelivet, i syntesen av makromolekyler, under studiet av kunstig intelligens. Og det er alt takket væreutvidelse av vår bevissthet, bort fra enkel addisjon og subtraksjon av naturverdier.