Blant hovedkartene til kart over området er dette oftest trukket frem. Dette er skaleringsnøyaktighet. I artikkelen vil vi analysere hva dette konseptet skjuler i seg selv. Vi vil også vurdere hva en skala er generelt, vi vil karakterisere hovedvariantene. La oss analysere hvordan konseptet "grafisk nøyaktighet" er relatert til emnet for samtalen vår.
Hva er dette?
Skala er en viktig avklaring som viser hvor mye hver linje som ble tegnet på tegningen, planen, er mindre eller mer enn den faktiske størrelsen på objektet den viser. Slike avklaringer presenteres på tegningsdokumenter og kart både numerisk og grafisk.
Skala av planer, nøyaktighet av skala - konsepter som kan finnes i en lang rekke områder:
- kartografi.
- Design.
- Geodesi.
- Foto.
- Modellering.
- Programmering.
- Math.
- Kino.
Noen av disse applikasjonene, deres funksjoner, vil vi vurdere i løpet av artikkelen.
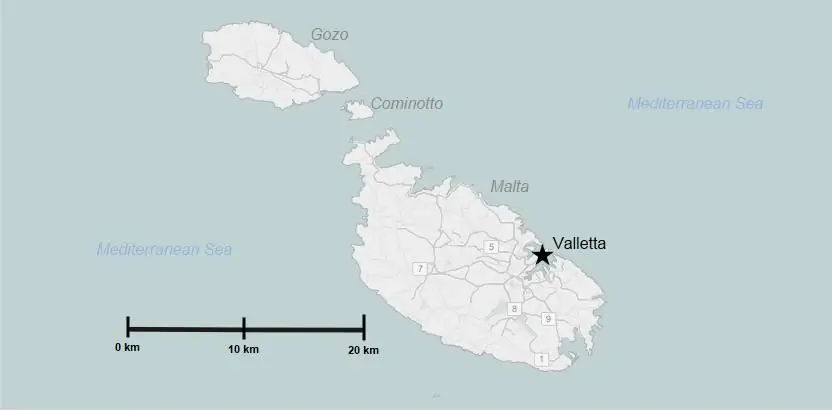
Skaleringsnøyaktighet
Og nådefinisjon av nøkkelbegrepet. Skaleringsnøyaktighet - en del av den horisontale linjeavstanden, som vil bety 0,1 mm på tegningen. Hvorfor ble denne verdien valgt?
0, 1 mm er akseptert her på grunn av det faktum at dette er det minste segmentet som kan skilles fra det menneskelige øyet i bildet uten bruk av spesialutstyr, verktøy, enheter.
La oss ta et konkret eksempel. Gitt 1:10000. Skalaens nøyaktighet vil være henholdsvis 1 m. La oss analysere nærmere:
- 1 cm på en plan eller et bilde er 10 000 cm (eller 100 m) på det virkelige terrenget.
- 1 mm i bildet er 1000 cm (eller 10 m).
- 0, 1 mm er 100 cm (eller 1 m) i ekte terreng.
Dermed er det enkelt å bestemme den maksimale nøyaktigheten til skalaen. Dette er avstanden til den virkelige overflaten, lik 0,1 mm på kartet - minimumssegmentet som en person kan skille.
Graphic fidelity
Og la oss nå bli kjent med den grafiske nøyaktigheten til skalaer. Dette er en annen viktig funksjon når du bruker planer og kart.
Grafisk nøyaktighet er assosiert med oppløsningen "og" til det menneskelige øyet. I sin tur gjør det "G". Derfor G=u.
Det vil si at hvis vinkelen "og" mellom vektorene inn i to punkter "B" og "L" når de sees av en observatør med norm alt synsnivå er "G" eller mer, vil de bli oppfattet som to punkter. Hvis denne vinkelen til oppløsningsbegrepet er mindre enn "G", vil "L" og "B" bli oppfattet av en person som enprikk.
Det er best å sette seg inn i definisjonen av skala nøyaktighet på et spesifikt eksempel. La oss si at en person undersøker kartet fra den beste avstanden "b", lik 35 cm. Verdien av G=u. Nå må du bestemme den minste avstanden (det vil si grafisk nøyaktighet) mellom "B" og "L", der de fortsatt vil bli oppfattet av observatøren som to forskjellige punkter. Her er regnestykket:
1 - er! - 1/3438 x 350 mm=0,1 mm.
1/3438 er verdien av vinkelen u=r, som i dette tilfellet uttrykkes i radianer (3438' er antall minutter i en radian).
Dermed er utgangsverdien på 0,1 mm den grafiske nøyaktigheten til planen eller kartet.
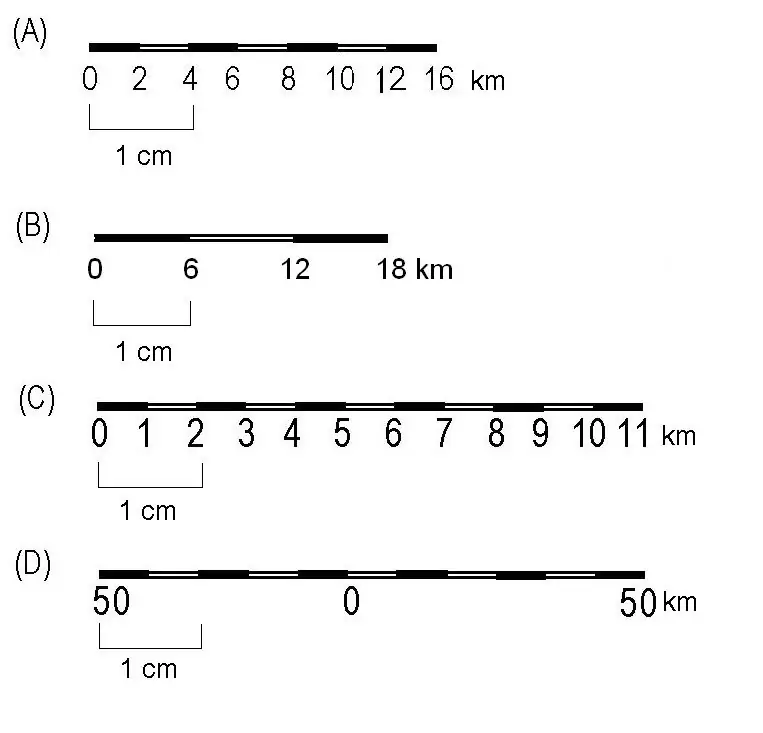
Kobling av konsepter
La oss nå se hvordan begrepet ovenfor relaterer seg til det viktigste. Nøyaktigheten til skalaen er, som vi husker, avstanden på jordoverflaten, som er lik 0,1 mm på dokumentet.
Du kan utlede formelen:
T=gM=0,1 M mm.
Dechiffrer elementene:
- T - skaleringsnøyaktighet.
- M er skala-nevneren.
- r=0,1 mm - grafisk nøyaktighet.
Herfra kan vi utlede den relaterte tolkningen. Skaleringsnøyaktighet - grafisk nøyaktighet, som uttrykkes i målestokken til et kart eller en plan. Og hva er resultatet? Grafisk nøyaktighet vil bli en konstant (0,1 mm) for alle eksisterende skalaer.
Følgelig vil skalaens nøyaktighet endres med den. Den blir jo høyere jo større kompilatoren valgte skalaen.
Og nåvi vil ta for oss trekk ved en slik karakteristikk som skala i ulike bruksområder.
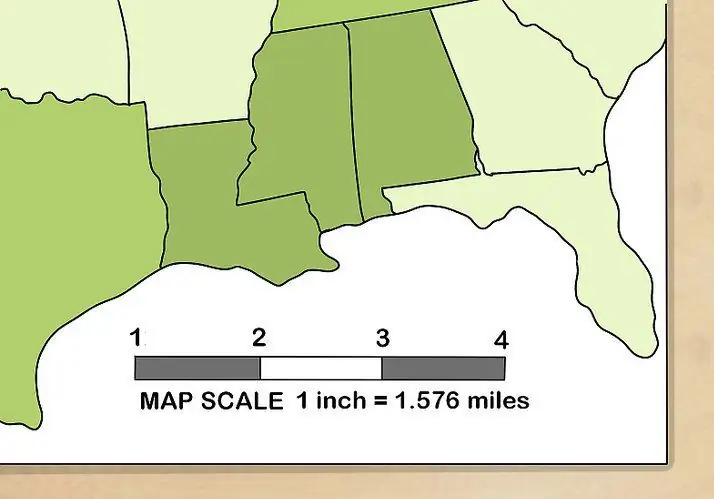
Design, geodesi og kartografi
Vi vet hva "500"-skala-nøyaktighet betyr - 1:500. La oss nå vurdere hvilke varianter av det som er typiske for feltet design, kartografi og geodesi:
- Numerisk skala. Indikatoren skrives som en brøk. Telleren vil være én, og nevneren vil være en viss grad av projeksjonsreduksjon på kartet. La oss for eksempel ta en målestokk på 1: 5 000. Det betyr at 1 cm på en plan, kart er 5 000 cm (eller 50 m) på et ekte terreng. Følgelig vil det være en større skala som har en mindre nevner. Så 1:1000 vil være større enn 1:20 000.
- Navnet skala. Kompilatoren av kartet foreskriver på dokumentet hvilken avstand på det virkelige terrenget som er lik 1 cm på planen. Her er et eksempel: "Det er 1000 kilometer på 1 centimeter". Eller kort sagt: "1 cm=100 km".
- Grafisk skala. I sin tur vil den deles inn i tverrgående og lineær. Vi vil analysere dem separat.

varianter av grafisk kategori
Hva er nøyaktigheten av skalaen - tverrskalaen? La oss bli kjent med egenskapene:
- Lineær. En slik grafisk målestokk på kartet er representert som en linjal, som vil deles inn i reelle deler.
- Tverrgående. Dette er en grafisk skala representert som et nomogram. Konstruksjonen er basert på proporsjonaliteten til delene av parallelle linjer som skjærer sidene av vinkelen. Denne skalaen er anvendelig for en mer nøyaktig måling av lengden på linjene på planene. De bruker det på denne måten: de måler lengden på den nederste linjen av en gitt tverrskala slik at den høyre enden er på en hel avstand (OM), og den venstre er forbi 0. Hvis i dette tilfellet venstre ben er mellom henholdsvis tiende avdelinger av venstre segment (fra 0), så løfter spesialisten begge bena på måleren opp. Inntil venstre ben av måleren allerede er i skjæringspunktet mellom en horisontal linje og en eventuell tverrgående. Men høyre bein skal også være på denne horisontale linjen. Minimum CD her er 0,2 mm. Følgelig er den minste nøyaktigheten 0,1 mm.
Serie med bildeskalaer i design
Vi vet allerede hva presisjon i skala 1:500 betyr. Men i hvilke tilfeller velger kompilatoren det? La oss analysere dette spørsmålet:
- Skalering ned. Følgelig brukes de i tilfeller der det er nødvendig å skildre et objekt på en plan, et terreng som betydelig overskrider det i området. Hvis kompilatoren vender seg til utformingen av hovedplaner av spesielt store størrelser, må han bruke følgende skalaer: 1:2 000, 1:5 000, 1:10 000, 1:20 000, 1:25 000, 1:50 000.
- Faktisk størrelse. Hvis du ønsker å avbilde objektet på planen "som det er", så referer til skalaen "en til en". Følgelig vil 1 cm reell lengde her tilsvare 1 cm lengde på planen.
- Vektforstørrelse. Nødvendig i tilfeller hvor det er nødvendig å avbilde et objekt som er for lite på planen for en detaljert bekjentskap med utseendet, enhet.
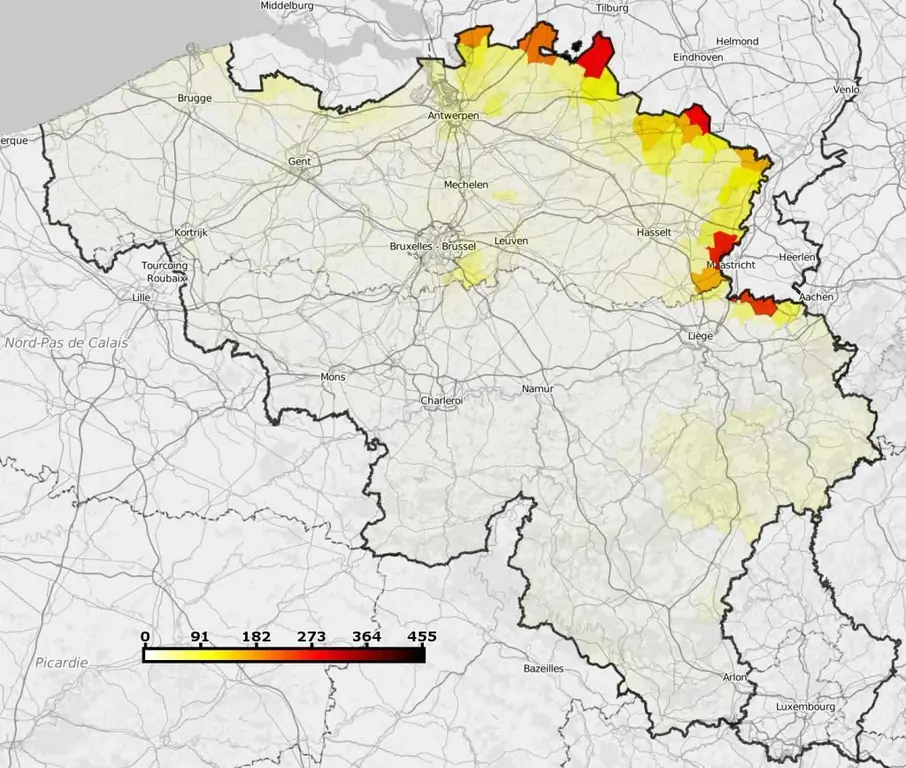
I bilde
Selvfølgelig er 1:10 000 skala nøyaktighet mer assosiert med kartografi. Men dette gjelder også fotografiets verden. Skalaen betyr her forholdet mellom de såk alte lineære dimensjonene til bildet oppnådd på en ultrasensitiv matrise eller på fotografisk film og størrelsen på projeksjonen av den tilsvarende projeksjonssonen på et plan som er vinkelrett på kameraet.
Det finnes fotografer som måler skalaen som forholdet mellom størrelsen på et ekte objekt og størrelsen på en skjerm, fotopapir eller andre medier. Men den riktige måten å bestemme skalaen på et fotografi avhenger bare av konteksten bildet brukes i.
I fotografering er skalaen også viktig når man beregner dybden til ethvert skarpt avbildet objekt, rom. I dag har spesialister tilgang til et veldig bredt spekter av skalaer fra uendelig små (brukes ved fotografering av fjerne himmellegemer) til veldig store (uten bruk av spesielle optiske vedlegg, for eksempel er det i dag mulig å få et bilde i skala 10:1).
Her anses makrofotografering allerede for å fotografere i en skala fra 1:1 (og følgelig større). Men med utbredelsen av digitale kompaktkameraer har makrofotografering også blitt k alt stilen når objektivet er plassert for nært motivet. Med tanke på den klassiske definisjonen, altsåen slik tolkning ville ikke være riktig.
I modellering
For hver type benk (eller skala) modellering er dets egne skalaer definert. De består av flere skalaer preget av en viss grad av reduksjon. Interessant nok er det for hver type modellering (jernbane, bil, skipsmodellering, militært utstyr, flymodellering) visse historisk utformede skalaserier som ikke krysser andre.
Her er skalaen beregnet med en enkel formel:
L / M=X.
Dechiffrer:
- L - originale parametere.
- M - skala kreves for arbeid.
- X er ønsket verdi.
I programmering
I dette området vil den såk alte tidsskalaen være viktig. La oss finne ut hva det er.
I et tidsdelings-OS er det svært viktig å gi "sanntid" til spesifikke oppgaver. Det skiller seg ved at behandlingen av eksterne hendelser går uten ytterligere forsinkelser eller hull. Her vil enda et konsept være viktig - «sanntidsskala». Men det skal forstås at det ikke har noen direkte relasjon til målestokken på kartene. Dette er bare en terminologisk konvensjon.
I filmteknologi
I filmteknologi er nøyaktigheten av tidsskalaen også viktig. Sistnevnte betyr en kvantitativ indikator for å bremse eller akselerere bevegelsen, som vil være lik forholdet mellom projeksjonsbildehastigheten og opptakshastigheten.
Vurder dette på en enkel måteeksempel. Projiseringsbildehastigheten for filmopptak er 24 fps. Filmingen ble utført samtidig "med en hastighet" på 72 bilder/sek. Tidsskalaen i dette tilfellet vil være 1:3.
Og hva vil for eksempel bety 2:1? Dette er dobbelt så raskt som standardflyten av det som skjer på skjermen.
I matematikk
I dette området refererer skala til det lineære forholdet mellom to dimensjoner. I mange praktisk anvendelige områder vil dette også være forholdet mellom bildestørrelsen og den faktiske størrelsen på bildet.
I matematikk er skalaen forholdet mellom en hvilken som helst avstand på kartet og den virkelige avstanden i det virkelige terrenget. Hvis vi ser på eksempelet, er dette det samme som i kartografi. La oss si 1:100 000 000. Så 1 cm i bildet er 100 000 cm i virkeligheten. Det vil si tusen meter eller én kilometer.
Skala er en allment anvendelig egenskap. Dette er en standard og integrert komponent i utviklingen av planer, tegninger av objekter, kart over området. Den brukes i design, i geodesi, kartografi, relevant innen fotografi, filmteknologi, programmering og matematikk. Den i seg selv er hovedsakelig preget av nøyaktighet - forholdet mellom den reelle avstanden og den aksepterte på kartet.






