For hvert år øker interessen for programmering. Og hvis de i institusjoner som spesialiserer seg på å skrive programmer, er avhengige av et slikt programmeringsspråk som C ++, blir studentene på skoler og tekniske skoler kjent med "Pascal". Og allerede på grunnlag av dette språket begynner de å forstå programmering gjennom bruk av Delphi-programvare. Det skal bemerkes med en gang at disse programmeringsspråkene gir et stort rom for manifestasjonen av fantasien deres. Og hvis du ved hjelp av Pascal-språket kan bli kjent med de grunnleggende konseptene for programmering, kan du allerede i Delphi skrive et fullverdig program. Og en ganske viktig plass i å skrive programmer er noen ganger okkupert av å løse arrays i "Pascal".
Tilstedeværelsen av et stort antall svært forskjellige variabler

Det er ganske mange forskjellige variabler i et programmeringsspråk, som er preget av tilstedeværelsen av bare én verdi. De er i stand til å lagre en enkelt verdi som har en bestemt type. Strengvariabler er unntaket. De erer en samling av de dataene som karaktertypen er karakteristisk for. Men selv slike variabler vurderes vanligvis fra posisjonen til en egen verdi.
Det er ingen hemmelighet at du ved hjelp av en datamaskin kan redusere tiden det tar å utføre visse oppgaver knyttet til store datamengder betydelig. Men hvordan, når du bare bruker de variablene som har typer kjent for mennesker, er det mulig å lagre resultatene av arbeidet i minnet, og også behandle de dataene som inneholder et stort antall rader? Slike oppgaver er ganske vanlige i alle aktivitetsfelt.
Selvfølgelig kan du alltid legge inn så mange variabler du trenger for å nå målene dine. Du kan også definere noen verdier for dem. Men koden til programmet vil bare øke fra dette. Det er vanskelig å lese koden som har et stort antall linjer. Spesielt når det er nødvendig å finne feil.
Følgelig tenkte programmererne på dette spørsmålet. Det er derfor språkene som er utviklet så langt har slike variabler som gjør det mulig å lagre en enorm mengde data i seg selv. Arrayen i «Pascal» har endret seg mye i tilnærmingen til programmering. Derfor anses den som en viktig variabel i et programmeringsspråk.
Bruk av matriser kan redusere kodestørrelsen drastisk
Under dette begrepet er det skjult en ordnet sekvens av data, som er preget av én type. I tillegg får alle disse dataene samme navn. Det burde det ogsåDet skal bemerkes at mange gjenstander i den virkelige verden kan passe til denne definisjonen: ordbøker, tegneserier og mye mer. Den enkleste måten å presentere en matrise på i "Pascal" er imidlertid i form av en slags tabell. Hver enkelt celle inneholder én variabel. Ved å bruke koordinater kan du bestemme posisjonen til variabelen som den vil oppta i den generelle tabellen.
Hva betyr en endimensjonal matrise?
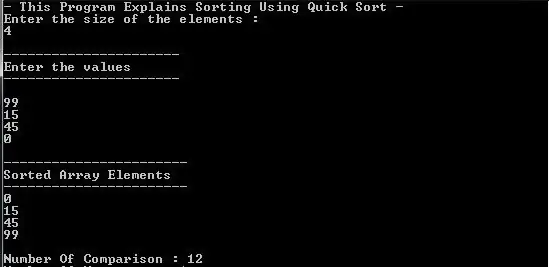
Den enkleste tabellen er den som er lineær. I denne matrisen, for å bestemme plasseringen av parameteren, er det nok å spesifisere bare ett tall. Mer komplekse matriser dannes basert på dem.
For å beskrive endimensjonale arrays i "Pascal", skriv inn følgende kode: Type Array of.
Tallene er de variablene som kan ha en ordin altype. Når du spesifiserer et område, er det verdt å forstå at det første tallet ikke kan være høyere enn det siste. Typen som array-elementene har kan være absolutt hva som helst - enten standard eller allerede tidligere beskrevet. Valget vil avhenge av behovet for å løse et bestemt problem.
Hvordan beskrives en lineær matrise?
Det er mulig å umiddelbart beskrive endimensjonale arrays i "Pascal". Dette må gjøres i en spesiell seksjon, som er nødvendig for denne spesielle prosedyren. Du må angi følgende kode: Var: Array Of.
For å forstå hvordan du kan beskrive en matrise i Pascal, bør du skrive inn følgende kode:
- Var
- S, VV: Array[5..50] Of Real;
- K: Array['C'.. 'R'] Of Heltall;
- Z: Array [-10..10] Of Word;
- E: Array [3..30] Of Real.
I dette eksemplet er variablene S, VV og T en matrise av de tallene som er reelle. Variabelen K skjuler tegntypen og disse elementene. Som er heltall. Z-matrisen lagrer tall med typen Word.
Blant alle handlingene som kan brukes når man jobber med en array, kan oppgave skilles. Hele bordet kan utsettes for det. For eksempel, S:=VV. Men det skal forstås at oppdragsoperasjoner bare kan utsettes for en matrise i "Pascal" som har en bestemt type.
Det er ikke flere operasjoner som kan utføres på hele matrisen samtidig. Du kan imidlertid arbeide med elementer på samme måte som med andre primtall som har en bestemt type. For å referere til en individuell parameter, må du spesifisere navnet på matrisen. Ved å bruke firkantede parenteser må du bestemme indeksen som er karakteristisk for ønsket element. For eksempel: K[12].
Hovedforskjeller mellom matriser og andre variabler
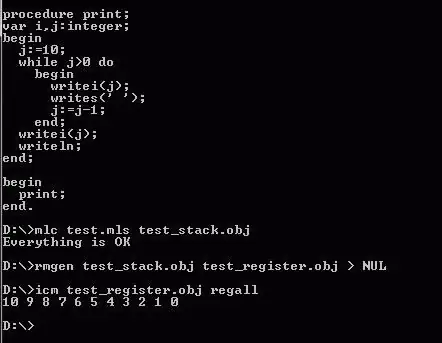
Den grunnleggende forskjellen mellom tabellkomponenter og enkle variabler er at det er mulig å sette i parentes ikke bare indeksverdien, men også et slikt uttrykk som kan føre til ønsket verdi. Et eksempel på indirekte adressering kan være: V[K]. I dette tilfellet får variabelen K en viss verdi. Fra dettedet følger at du kan bruke en løkke når du fyller, behandler og skriver ut en matrise.
Denne organisasjonsformen kan forekomme når det gjelder strengvariabler som er nær nok i egenskapene til matriser av typen Char. Men det er også forskjeller. De er som følger:
- Strengvariabler kan alltid legges inn fra tastaturet og skrives ut på skjermen.
- Strengvariabler er begrenset i lengde. Du kan skrive inn maksim alt 255 tegn. Den kritiske størrelsen på matrisen er 64 kb.
Hvilke metoder kan brukes for å vise matrisedata på skjermen?
Du bør være oppmerksom på måten innholdet i matrisen vises på. Det er flere.
- Writeln (A[1], A[2], A[3]). Et slikt eksempel, selv om det er primitivt, er i stand til å vise hvordan du kan få direkte tilgang til hvert enkelt element som er iboende i tabellen. Noen av fordelene som Pascal-matriser har fremfor enkle variabler er imidlertid ikke synlige her.
-
Program A1;
Var B: Array [1..10] Of Integer;
K: Integer;
Begin
For K:=1 Til 10 Gjør {Denne kommandoen går i sløyfe med parameter }
Readln(A[K]); {A[I] legges inn med tastaturet }
For K:=10 Ned til 1 Gjør {Tabellen skrives ut i omvendt rekkefølge}
Skriv(A[K], 'VVV') End.
En lignende kode for programmet for arrays i "Pascal" demonstrerer hvordan du kan skrive inn 10 tall ved hjelp av tastaturet, skrive dem ut, omorganisere verdiene i omvendt rekkefølge. Hvis det samme programmet skrives om fraved å bruke et stort antall variabler i stedet for en matrise, vil koden økes betydelig. Og dette kompliserer prosessen med å lese programmet i stor grad.
Øke muligheter gjennom bruk av arrays

Det er også mulig å fylle tabeller med verdier som er lik kvadratet av elementindekser. Det er også mulig å lage en slik rekke strenger i "Pascal", som vil tillate at alle tall legges inn automatisk. Som du kan se, forbedrer bruk av en array funksjonene til Pascal-programmeringsspråket betraktelig.
Behandling av lineære arrays er svært vanlig i ulike oppgaver. Derfor er det ikke noe rart i at de studeres på institutter og skoler. I tillegg er mulighetene som arrays har ganske omfattende.
Hva er skjult under todimensjonale arrays?
Du kan tenke deg en tabell som består av flere rader samtidig. Hver enkelt rad inneholder flere celler. I en slik situasjon, for å nøyaktig bestemme posisjonen til cellene, er det nødvendig å ikke merke en indeks, som tilfellet var med lineære matriser, men to - tall som er karakteristiske for en rad og en kolonne. Todimensjonale arrays i "Pascal" er preget av en lignende representasjon.
Hvordan beskrive tabeller av denne typen?
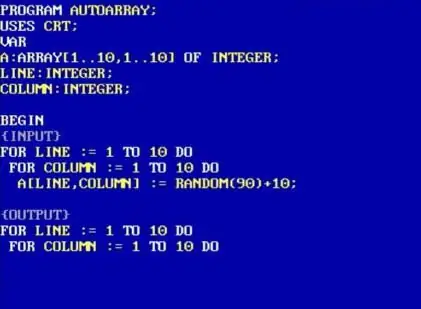
Datastrukturen som finnes i Pascal-språket for å lagre verdiene til en slik tabell ernavnet på en todimensjonal matrise. Beskrivelse av en slik matrise er mulig umiddelbart ved å bruke to metoder.
- Var B: Array[1..15] Of Array [1..30] Of Integer;
- Var B: Array [1..15, 1..30] Of Integer.
I alle disse tilfellene beskrives en todimensjonal matrise som har 15 rader og 30 kolonner. De beskrivelsene som ble gitt ovenfor er absolutt likeverdige. For å begynne å jobbe med ett av elementene, er det nødvendig å tildele to indekser. For eksempel A[6][5] eller A[6, 5].
Utgangen til skjermen vil være nesten den samme som for en endimensjonal matrise. Du trenger bare å spesifisere to indekser. I alle andre henseender er det ingen forskjeller som sådan, så det er ikke nødvendig å snakke lenge om det.
Første måte å sortere på
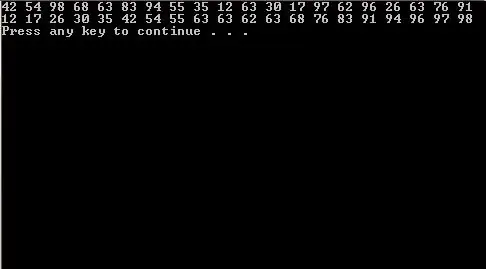
Noen ganger blir det nødvendig å sortere data. For dette har språket tilsvarende kommandoer. Det er to algoritmer som en matrise kan sorteres med i Pascal. Betydningen av den direkte seleksjonsmetoden ligger i det faktum at ved å neste løkken, vil absolutt hver tabellvariabel bli sammenlignet med andre verdier. Med andre ord, hvis det er en matrise med 15 tall, vil første nummer 1 bli sammenlignet med andre tall. Dette vil skje til for eksempel elementet som er større enn det første tallet er funnet. Deretter vil sammenligningen finne sted akkurat dette tallet. Dette gjentas til den største er funnet.element fra alle foreslåtte. Denne metoden er ganske enkel for programmerere som nettopp har begynt å jobbe med språket.
Sorteringsmetode for andre array
Den andre måten er boble. Essensen av denne teknikken ligger i det faktum at naboelementer sammenlignes i par. For eksempel, 1 og 2, 2 og 3, 3 og 4 osv. I tilfelle at den funnet verdien fullt ut samsvarer med sorteringsbetingelsene, vil den bli flyttet til slutten av hele matrisen, dvs. den vil dukke opp som en "boble". Denne algoritmen er den vanskeligste å huske. Du trenger imidlertid ikke slipe den. Det viktigste er å forstå hele strukturen til koden. Og bare i dette tilfellet kan man hevde å oppnå store høyder i programmering.
Konklusjon

Vi håper du forstår hva arrays er og hvordan du kan sortere for å finne en bestemt verdi eller oppnå et spesifikt mål. Hvis du har valgt "Pascal" for å løse et bestemt problem, der matriser opptar en viktig plass, må du nærme deg studien deres grundig. Dette påvirkes av en slik faktor som tilstedeværelsen på språket av et tilstrekkelig stort antall variabler som brukes i visse situasjoner for å forenkle hele koden som helhet. Arrays regnes med rette som hovedmengdene, og studiet av disse må finne sted uten feil.






